题目内容
(12分) 季节性服装当季节即将来临时,价格呈上升趋势,设某服装开始时定价为10元,并且每周(7天)涨价2元,5周后开始保持20元的价格平稳销售;10周后当季节即将过去时,平均每周削价2元,直到16周末,该服装已不再销售.
(1)试建立价格P与周次t之间的函数关系式.
(2)若此服装每件进价![]() 与周次t之间的关系为
与周次t之间的关系为![]() ,
,
试问该服装第几周每件销售利润L最大?(注:每件销售利润=售价-进价)
解:(1) 由题意知:
当t∈[0,5]且t∈N时,P=10+2t ……………………………………1分
当t∈(5,10]且t∈N时,P=20 …………………………………………2分
当t∈(10,16]且t∈N时,P=20-![]() =
=![]() …………………3分
…………………3分
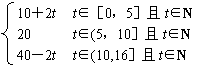 | |||
| |||
![]() 综上P=
综上P=
(2)因为每件销售利润=售价-进价,即L=P-Q,则
①当t∈[0,5]且t∈N时,L=10+2t+![]() (t-8)2-12=
(t-8)2-12=![]() t2+6
t2+6
![]() t=5时,Lmax=
t=5时,Lmax=![]() ……………………………………………………………………6分
……………………………………………………………………6分
②当t∈(5,10]且t∈N时,L=20+![]() (t-8)2-12 =
(t-8)2-12 = ![]() (t-8)2 +8
(t-8)2 +8
![]() t=6或10时,Lmax=
t=6或10时,Lmax=![]() ……………………………………………………………8分
……………………………………………………………8分
③当t∈(10,16]且t∈N时,L=40-2t+![]() (t-8)2-12=
(t-8)2-12=![]() (t-16)2 +4
(t-16)2 +4
![]() t=11时,Lmax=
t=11时,Lmax=![]() ……………………………………………………………10分
……………………………………………………………10分
综上由①②③得,当t∈[0,16]且t∈N时,Lmax=![]() …………………………11分
…………………………11分
所以该服装第5周每件销售利润L最大 …………………………………12分

 53随堂测系列答案
53随堂测系列答案