摘要:(14) ,提示:∵..∴(15)6, 提示: 用秦九韶算法.将原式变形为
网址:http://m.1010jiajiao.com/timu_id_256680[举报]
观察下列不等式:
①
<1;
②
+
<
;
③
+
+
<
;…
则第5个不等式为
+
+
+
+
<
+
+
+
+
<
.
查看习题详情和答案>>
①
| 1 | ||
|
②
| 1 | ||
|
| 1 | ||
|
| 2 |
③
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 3 |
则第5个不等式为
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 5 |
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 5 |
观察等式:
+
=
,
+
+
=
,
+
+
+
=
,
根据以上规律,写出第四个等式为:
+
+
+
+
=
+
+
+
+
=
.
查看习题详情和答案>>
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 2 |
| 3 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 3 |
| 4 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 4×5 |
| 4 |
| 5 |
根据以上规律,写出第四个等式为:
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 4×5 |
| 1 |
| 5×6 |
| 5 |
| 6 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 4×5 |
| 1 |
| 5×6 |
| 5 |
| 6 |
杨辉是中国南宋末年的一位杰出的数学家、数学教育家、杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,杨辉三角中蕴藏了许多优美的规律.如图是一个11阶杨辉三角:
(1)求第20行中从左到右的第4个数;
(2)若第n行中从左到右第14与第15个数的比为
,求n的值;
(3)求n阶(包括0阶)杨辉三角的所有数的和;
(4)在第3斜列中,前5个数依次为1,3,6,10,15;第4斜列中,第5个数为35.显然,1+3+6+10+15=35.事实上,一般地有这样的结论:第m斜列中(从右上到左下)前k个数之和,一定等于第m+1斜列中第k个数.试用含有m、k(m,k∈N×)的数学公式表示上述结论,并给予证明.
查看习题详情和答案>>
(1)求第20行中从左到右的第4个数;
(2)若第n行中从左到右第14与第15个数的比为
| 2 |
| 3 |
(3)求n阶(包括0阶)杨辉三角的所有数的和;
(4)在第3斜列中,前5个数依次为1,3,6,10,15;第4斜列中,第5个数为35.显然,1+3+6+10+15=35.事实上,一般地有这样的结论:第m斜列中(从右上到左下)前k个数之和,一定等于第m+1斜列中第k个数.试用含有m、k(m,k∈N×)的数学公式表示上述结论,并给予证明.
| 第0行 | 1 | … | … | … | … | … | … | … | … | … | … | … | … | 第1斜列 | |||||||||||
| 第1行 | 1 | 1 | … | … | … | … | … | … | … | … | … | … | … | 第2斜列 | |||||||||||
| 第2行 | 1 | 2 | 1 | … | … | … | … | … | … | … | … | … | … | 第3斜列 | |||||||||||
| 第3行 | 1 | 3 | 3 | 1 | … | … | … | … | … | … | … | … | … | 第4斜列 | |||||||||||
| 第4行 | 1 | 4 | 6 | 4 | 1 | … | … | … | … | … | … | … | … | 第5斜列 | |||||||||||
| 第5行 | 1 | 5 | 10 | 10 | 5 | 1 | … | … | … | … | … | … | … | 第6斜列 | |||||||||||
| 第6行 | 1 | 6 | 15 | 20 | 15 | 6 | 1 | … | … | … | … | … | … | 第7斜列 | |||||||||||
| 第7行 | 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | … | … | … | … | … | 第8斜列 | |||||||||||
| 第8行 | 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | … | … | … | … | 第9斜列 | |||||||||||
| 第9行 | 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 | … | … | … | 第10斜列 | |||||||||||
| 第10行 | 1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 | … | … | 第11斜列 | |||||||||||
| 第11行 | 1 | 11 | 55 | 165 | 330 | 462 | 462 | 330 | 165 | 55 | 11 | 1 | … | 第12斜列 | |||||||||||
| 11阶杨辉三角 | |||||||||||||||||||||||||
下表是某省的20个县城2006年的一份统计资料,其中![]() 表示第i个县城在2006年建成的新住宅的面积(单位:万平方米),
表示第i个县城在2006年建成的新住宅的面积(单位:万平方米),![]() 表示第i个县城在2006年的家具销售额(单位:万元)
表示第i个县城在2006年的家具销售额(单位:万元)
| 县城编号 | xi | yi | 县城编号 | xi | yi |
| 1 | 121 | 360 | 11 | 387 | 602 |
| 2 | 118 | 260 | 12 | 270 | 540 |
| 3 | 271 | 440 | 13 | 218 | 414 |
| 4 | 190 | 400 | 14 | 342 | 590 |
| 5 | 75 | 360 | 15 | 173 | 492 |
| 6 | 263 | 500 | 16 | 370 | 660 |
| 7 | 334 | 580 | 17 | 170 | 360 |
| 8 | 368 | 560 | 18 | 205 | 410 |
| 9 | 305 | 505 | 19 | 339 | 680 |
| 10 | 210 | 480 | 20 | 283 | 594 |
试求![]() 对
对![]() 的回归方程.
的回归方程.
(13分)
某研究机构为了研究人的脚的大小(码)与身高(厘米)之间的关系,随机抽测了20人,得到如下数据:
|
序号 |
身高x |
脚长y |
序号 |
身高x |
脚长y |
|
1 |
176 |
42 |
11 |
179 |
44 |
|
2 |
175 |
44 |
12 |
169 |
43 |
|
3 |
174 |
41 |
13 |
185 |
45 |
|
4 |
180 |
44 |
14 |
166 |
40 |
|
5 |
170 |
42 |
15 |
174 |
42 |
|
6 |
178 |
43 |
16 |
167 |
42 |
|
7 |
173 |
42 |
17 |
173 |
41 |
|
8 |
168 |
40 |
18 |
174 |
42 |
|
9 |
190 |
46 |
19 |
172 |
42 |
|
10 |
171 |
42 |
20 |
175 |
41 |
(1)若“身高大于175厘米”的为“高个”,“身高小于等于175厘米”的为“非高个”,“脚长大于42码”的为“大脚”,“脚长小于等于42码”的为“非大脚”.请根据上表数据完成如下2×2列联表;
|
|
高个 |
非高个 |
合计 |
|
大脚 |
|
|
|
|
非大脚 |
|
12 |
|
|
合计 |
|
|
20 |
(2)根据题(1)中表格的数据,若按99%的可靠性要求,能否认为脚的大小与身高有关系? 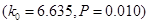
查看习题详情和答案>>