题目内容
下表是某省的20个县城2006年的一份统计资料,其中![]() 表示第i个县城在2006年建成的新住宅的面积(单位:万平方米),
表示第i个县城在2006年建成的新住宅的面积(单位:万平方米),![]() 表示第i个县城在2006年的家具销售额(单位:万元)
表示第i个县城在2006年的家具销售额(单位:万元)
| 县城编号 | xi | yi | 县城编号 | xi | yi |
| 1 | 121 | 360 | 11 | 387 | 602 |
| 2 | 118 | 260 | 12 | 270 | 540 |
| 3 | 271 | 440 | 13 | 218 | 414 |
| 4 | 190 | 400 | 14 | 342 | 590 |
| 5 | 75 | 360 | 15 | 173 | 492 |
| 6 | 263 | 500 | 16 | 370 | 660 |
| 7 | 334 | 580 | 17 | 170 | 360 |
| 8 | 368 | 560 | 18 | 205 | 410 |
| 9 | 305 | 505 | 19 | 339 | 680 |
| 10 | 210 | 480 | 20 | 283 | 594 |
试求![]() 对
对![]() 的回归方程.
的回归方程.
见解析
解析:
解:新建成住房当然要添置新家具,这是人们的普遍心理,因此建成的住宅越多,家具的销售量就会越多,把上面的20个县城的统计资料表示在图上,横坐标表示新建成的住宅的面积,纵坐标表示对应的家具销售量。从散点图上可以看出上述规律。

由于家具销售量与新住宅落成的面积间呈线性相关关系,所以我们可以用回归直线去描述它。由已知数据可以算出:
![]() ,
,![]()
从而![]() ,
,![]() ,从而所求的回归方程为:
,从而所求的回归方程为:![]()

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
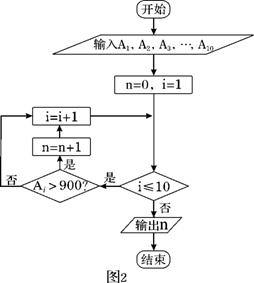
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案 下表是某工厂10个车间2011年3月份产量的统计表,1到10车间的产量依次记为A1,A2,…,A10(如:A6表示6号车间的产量为980件).图2是统计下表中产量在一定范围内车间个数的一个算法流程图.那么算法流程(图2)输出的结果是( ) 下表是某工厂10个车间2011年3月份产量的统计表,1到10车间的产量依次记为A1,A2,…,A10(如:A6表示6号车间的产量为980件).图2是统计下表中产量在一定范围内车间个数的一个算法流程图.那么算法流程(图2)输出的结果是( )
|
下表是某工厂10个车间2011年3月份产量的统计表,1到10车间的产量依次记为 (如:
(如: 表示6号车间的产量为980件).图2是统计下表中产量在一定范围内车间个数的一个算法流程图.那么算法流程图2输出的结果是 .
表示6号车间的产量为980件).图2是统计下表中产量在一定范围内车间个数的一个算法流程图.那么算法流程图2输出的结果是 .
|
车间 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
产量 |
1080 |
900 |
930 |
850 |
1500 |
980 |
960 |
900 |
830 |
1250 |

下表是某工厂10个车间2011年3月份产量的统计表,1到10车间的产量依次记为 (如:
(如: 表示6号车间的产量为980件),图2是统计下表中产量在一定范围内车间个数的一个算法流程图,那么算法流程(图2)输出的结果是( ).
表示6号车间的产量为980件),图2是统计下表中产量在一定范围内车间个数的一个算法流程图,那么算法流程(图2)输出的结果是( ).
|
车间 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
产量 |
1080 |
900 |
930 |
850 |
1500 |
980 |
960 |
900 |
830 |
1250 |
A. 5 B.6 C. 4 D. 7
下表是某工厂10个车间2011年3月份产量的统计表,1到10车间的产量依次记为 (如:
(如: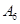 表示6号车间的产量为980件).图2是统计下表中产量在一定范围内车间个数的一个算法流程图.那么算法流程(图2)输出的结果是( )[来源:ZXXK]
表示6号车间的产量为980件).图2是统计下表中产量在一定范围内车间个数的一个算法流程图.那么算法流程(图2)输出的结果是( )[来源:ZXXK]
|
车间 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
产量 |
1080 |
900 |
930 |
850 |
1500 |
980 |
960 |
900 |
830 |
1250 |

A. 5 B. 6 C. 4 D. 7