摘要：(Ⅰ)求证:,(Ⅱ)求及数列的通项公式并证明,
网址：http://m.1010jiajiao.com/timu_id_254534[举报]
数列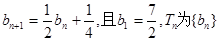
的前n项和。
（1）求证：数列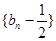
是等比数列，并求
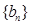的通项公式；
（2）如果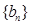对任意
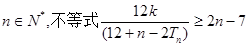恒成立，求实数k的取值范围。
【解析】本试题主要是考查了等比数列的定义的运用，以及运用递推关系求解数列通项公式的运用，并且能借助于数列的和，放缩求证不等式的综合试题。
查看习题详情和答案>>
数列{an}中，a1=2，an+1=an+2n+1（n∈N+）
（1）求证：数列{an-2n}是等差数列；
（2）求数列{an}的通项公式an及数列{an}的前n项和Sn；
（3）bn=log2（an+1-n），若（1+
）（1+
）…（1+
）＞k
对一切n≥2恒成立，求实数k的范围．
查看习题详情和答案>>
（1）求证：数列{an-2n}是等差数列；
（2）求数列{an}的通项公式an及数列{an}的前n项和Sn；
（3）bn=log2（an+1-n），若（1+
| 1 |
| b2 |
| 1 |
| b3 |
| 1 |
| bn |
| n+1 |
数列{an}是首项为2，公差为1的等差数列，其前n项和为Sn
（1）求数列{an}的通项公式an及前n项和为Sn；
（2）设log2bn=an-1，证明：
+
+…+
＜1．
查看习题详情和答案>>
（1）求数列{an}的通项公式an及前n项和为Sn；
（2）设log2bn=an-1，证明：
| 1 |
| b2-b1 |
| 1 |
| b3-b2 |
| 1 |
| bn+1-bn |
的前
项和
是
二项展开式中各项系数的和
． 
满足
，且
，求数列
的通
；
．