摘要：⑵对任意正整数n.不等式成立.求正数a的取值范围.
网址：http://m.1010jiajiao.com/timu_id_24510[举报]
设不等式
所表示的平面区域为Dn，记Dn内的格点(x，y)(x，y∈Z)的个数为f(n)(n∈N*)．（注：格点是指横坐标、纵坐标均为整数的点）
(Ⅰ)求f(1)，f(2)的值及f(n)的表达式；
(Ⅱ)记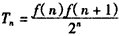
，若对于任意n∈N*，总有Tn≤m成立，求实数m的取值范围；
(Ⅲ)设Sn为数列{bn}的前n项和，其中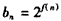
，问是否存在正整数n，t，使
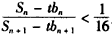成立，若存在，求出正整数n，t；若不存在，请说明理由．
查看习题详情和答案>>
所表示的平面区域为Dn，记Dn内的格点(x，y)(x，y∈Z)的个数为f(n)(n∈N*)．（注：格点是指横坐标、纵坐标均为整数的点）(Ⅰ)求f(1)，f(2)的值及f(n)的表达式；
(Ⅱ)记
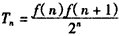，若对于任意n∈N*，总有Tn≤m成立，求实数m的取值范围；(Ⅲ)设Sn为数列{bn}的前n项和，其中
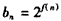，问是否存在正整数n，t，使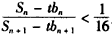成立，若存在，求出正整数n，t；若不存在，请说明理由． 已知正项数列{an}中，a1=6，点
在抛物线y2=x+1上；数列{bn}中，点Bn（n，bn）在过点（0，1），以方向向量为（1，2）的直线上．
（Ⅰ）求数列{an}，{bn}的通项公式；（文理共答）
（Ⅱ）若f（n）=
，问是否存在k∈N，使f（k+27）=4f（k）成立，若存在，求出k值；若不存在，说明理由；（文理共答）
（Ⅲ）对任意正整数n，不等式
≤0成立，求正数a的取值范围．（只理科答）
已知正项数列{an}中，a1=6，点
在抛物线y2=x+1上；数列{bn}中，点Bn（n，bn）在过点（0，1），以方向向量为（1，2）的直线上．
（Ⅰ）求数列{an}，{bn}的通项公式；（文理共答）
（Ⅱ）若f（n）=
，问是否存在k∈N，使f（k+27）=4f（k）成立，若存在，求出k值；若不存在，说明理由；（文理共答）
（Ⅲ）对任意正整数n，不等式
≤0成立，求正数a的取值范围．（只理科答）
查看习题详情和答案>>
在抛物线y2=x+1上；数列{bn}中，点Bn（n，bn）在过点（0，1），以方向向量为（1，2）的直线上．（Ⅰ）求数列{an}，{bn}的通项公式；（文理共答）
（Ⅱ）若f（n）=
，问是否存在k∈N，使f（k+27）=4f（k）成立，若存在，求出k值；若不存在，说明理由；（文理共答）（Ⅲ）对任意正整数n，不等式
≤0成立，求正数a的取值范围．（只理科答）查看习题详情和答案>>
在抛物线y2=x+1上；数列{bn}中，点Bn（n，bn）在过点（0，1），以方向向量为（1，2）的直线上．
，问是否存在k∈N，使f（k+27）=4f（k）成立，若存在，求出k值；若不存在，说明理由；（文理共答）
≤0成立，求正数a的取值范围．（只理科答）
在抛物线y2=x+1上；数列{bn}中，点Bn（n，bn）在过点（0，1），以方向向量为（1，2）的直线上．
，问是否存在k∈N，使f（k+27）=4f（k）成立，若存在，求出k值；若不存在，说明理由；（文理共答）
≤0成立，求正数a的取值范围．（只理科答）