题目内容
已知正项数列{an}中,a1=6,点![]() 在抛物线y2=x+1上;数列{bn}中,点Bn(n,bn)在过点(0,1),以方向向量为(1,2)的直线上.
在抛物线y2=x+1上;数列{bn}中,点Bn(n,bn)在过点(0,1),以方向向量为(1,2)的直线上.
(Ⅰ)求数列{an},{bn}的通项公式;(文理共答)
(Ⅱ)若f(n)= ,问是否存在k∈N,使f(k+27)=4f(k)成立,若存在,求出k值;若不存在,说明理由;(文理共答)
,问是否存在k∈N,使f(k+27)=4f(k)成立,若存在,求出k值;若不存在,说明理由;(文理共答)
(Ⅲ)对任意正整数n,不等式 ≤0成立,求正数a的取值范围.(只理科答)
≤0成立,求正数a的取值范围.(只理科答)
考点:
等差数列与等比数列的综合;等差数列的通项公式;等比数列的通项公式;数列与不等式的综合.
专题:
综合题;等差数列与等比数列.
分析:
(Ⅰ)将点![]() 代入抛物线y2=x+1,得an+1=an+1,由此能求出an;过点(0,1),以方向向量为(1,2)的直线方程为y=2x+1,把点Bn(n,bn)代入能求出bn.
代入抛物线y2=x+1,得an+1=an+1,由此能求出an;过点(0,1),以方向向量为(1,2)的直线方程为y=2x+1,把点Bn(n,bn)代入能求出bn.
(Ⅱ)由f(n)= =
=![]() ,利用题设条件能推导出存在唯一的k=4符合条件.
,利用题设条件能推导出存在唯一的k=4符合条件.
(Ⅲ)由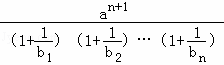 ﹣
﹣![]() ≤0,知a≤
≤0,知a≤![]() ,设f(n+1)=
,设f(n+1)=![]() ,利用构造法能求出正数a的取值范围.
,利用构造法能求出正数a的取值范围.
解答:
解:(Ⅰ)将点![]() 代入抛物线y2=x+1,
代入抛物线y2=x+1,
得an+1=an+1,
∴an+1﹣an=d=1,
∴an=a1+(n﹣1)•1=n+5,
∵过点(0,1),以方向向量为(1,2)的直线方程为y=2x+1,
点Bn(n,bn)在过点(0,1),以方向向量为(1,2)的直线上,
∴bn=2n+1.
(Ⅱ)由(Ⅰ)知f(n)= =
=![]() ,
,
当k为偶数时,k+27为奇数,
∴f(k+27)=4f(k),
∴k+27+5=4(2k+1),∴k=4.
当k为奇数时,k+27为偶数,
∴2(k+27)+1=4(k+5),∴k=![]() (舍去)
(舍去)
综上所述,存在唯一的k=4符合条件.
(Ⅲ)由 ﹣
﹣![]() ≤0,
≤0,
即a≤![]() ,
,
设f(n+1)=![]() ,
,
∴![]() =
=![]()
=![]()
=![]()
= ,
,
∴f(n+1)>f(n),即f(n)递增,
∴f(n)min=f(1)=![]() =
=![]() ,
,
∴0<a≤![]() .…(12分)
.…(12分)
点评:
本题考查数列的通项公式的求法,考查满足条件的实数的取值范围的求法,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

 名校课堂系列答案
名校课堂系列答案