网址:http://m.1010jiajiao.com/timu_id_24466[举报]
已知数列 满足
满足 (I)求数列
(I)求数列 的通项公式;
的通项公式;
(II)若数列 中
中 ,前
,前 项和为
项和为 ,且
,且 证明:
证明:
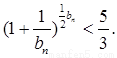
【解析】第一问中,利用 ,
,
∴数列{ }是以首项a1+1,公比为2的等比数列,即
}是以首项a1+1,公比为2的等比数列,即
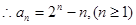
第二问中,

进一步得到得 即
即
即 是等差数列.
是等差数列.
然后结合公式求解。
解:(I) 解法二、 ,
,
∴数列{ }是以首项a1+1,公比为2的等比数列,即
}是以首项a1+1,公比为2的等比数列,即
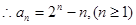
(II)
 ………②
………②
由②可得: …………③
…………③
③-②,得 即
即 …………④
…………④
又由④可得 …………⑤
…………⑤
⑤-④得
即 是等差数列.
是等差数列.




查看习题详情和答案>>
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1.
(Ⅰ)证明PC⊥AD;
(Ⅱ)求二面角A-PC-D的正弦值;
(Ⅲ)设E为棱PA上的点,满足异面直线BE与CD所成的角为30°,求AE的长.

【解析】解法一:如图,以点A为原点建立空间直角坐标系,依题意得A(0,0,0),D(2,0,0),C(0,1,0), 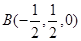 ,P(0,0,2).
,P(0,0,2).

(1)证明:易得 ,
, 于是
于是 ,所以
,所以
(2)  ,
, 设平面PCD的法向量
设平面PCD的法向量 ,
,
则 ,即
,即 .不防设
.不防设 ,可得
,可得 .可取平面PAC的法向量
.可取平面PAC的法向量 于是
于是 从而
从而 .
.
所以二面角A-PC-D的正弦值为 .
.
(3)设点E的坐标为(0,0,h),其中 ,由此得
,由此得 .
.
由 ,故
,故
所以, ,解得
,解得 ,即
,即 .
.
解法二:(1)证明:由 ,可得
,可得 ,又由
,又由 ,
, ,故
,故 .又
.又 ,所以
,所以 .
.

(2)如图,作 于点H,连接DH.由
于点H,连接DH.由 ,
, ,可得
,可得 .
.
因此 ,从而
,从而 为二面角A-PC-D的平面角.在
为二面角A-PC-D的平面角.在 中,
中, ,由此得
,由此得 由(1)知
由(1)知 ,故在
,故在 中,
中,
因此 所以二面角
所以二面角 的正弦值为
的正弦值为 .
.
(3)如图,因为 ,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF. 故
,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF. 故 或其补角为异面直线BE与CD所成的角.由于BF∥CD,故
或其补角为异面直线BE与CD所成的角.由于BF∥CD,故 .在
.在 中,
中, 故
故

在 中,由
中,由 ,
, ,
,
可得 .由余弦定理,
.由余弦定理, ,
,
所以 .
.
查看习题详情和答案>>
⊙O1和⊙O2的极坐标方程分别为 ,
, .
.
⑴把⊙O1和⊙O2的极坐标方程化为直角坐标方程;
⑵求经过⊙O1,⊙O2交点的直线的直角坐标方程.
【解析】本试题主要是考查了极坐标的返程和直角坐标方程的转化和简单的圆冤啊位置关系的运用
(1)中,借助于公式 ,
, ,将极坐标方程化为普通方程即可。
,将极坐标方程化为普通方程即可。
(2)中,根据上一问中的圆的方程,然后作差得到交线所在的直线的普通方程。
解:以极点为原点,极轴为x轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
(I) ,
, ,由
,由 得
得 .所以
.所以 .
.
即 为⊙O1的直角坐标方程.
为⊙O1的直角坐标方程.
同理 为⊙O2的直角坐标方程.
为⊙O2的直角坐标方程.
(II)解法一:由 解得
解得 ,
,
即⊙O1,⊙O2交于点(0,0)和(2,-2).过交点的直线的直角坐标方程为y=-x.
解法二: 由 ,两式相减得-4x-4y=0,即过交点的直线的直角坐标方程为y=-x
,两式相减得-4x-4y=0,即过交点的直线的直角坐标方程为y=-x
查看习题详情和答案>>
下面给出两种不同的解法.
解法一:∵P(A)=![]() ,P(B)=
,P(B)=![]() ,
,
∴P(A+B)=P(A)+P(B)=1.
解法二:A+B这一事件包括4种结果,即出现1,2,3和5,
∴P(A+B)=![]() .
.
请你判断解法一和解法二的正误.
查看习题详情和答案>>
已知向量 (
( ),向量
),向量 ,
, ,
,
且

 .
.
(Ⅰ)求向量 ;
(Ⅱ)若
;
(Ⅱ)若 ,
, ,求
,求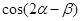 .
.
【解析】本试题主要考查了向量的数量积的运算,以及两角和差的三角函数关系式的运用。
(1)问中∵ ,∴
,∴ ,…………………1分
,…………………1分
∵ ,得到三角关系是
,得到三角关系是 ,结合
,结合 ,解得。
,解得。
(2)由 ,解得
,解得 ,
, ,结合二倍角公式
,结合二倍角公式 ,和
,和 ,代入到两角和的三角函数关系式中就可以求解得到。
,代入到两角和的三角函数关系式中就可以求解得到。
解析一:(Ⅰ)∵ ,∴
,∴ ,…………1分
,…………1分
∵ ,∴
,∴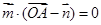 ,即
,即 ① …………2分
① …………2分
又 ② 由①②联立方程解得,
② 由①②联立方程解得,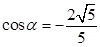 ,
,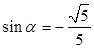 5分
5分
∴ ……………6分
……………6分
(Ⅱ)∵ 即
即 ,
, , …………7分
, …………7分
∴ ,
, ………8分
………8分
又∵ , ………9分
, ………9分
 , ……10分
, ……10分
∴ .
.
解法二: (Ⅰ) ,…………………………………1分
,…………………………………1分
又 ,∴
,∴ ,即
,即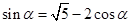 ,①……2分
,①……2分
又 ②
②
将①代入②中,可得 ③ …………………4分
③ …………………4分
将③代入①中,得 ……………………………………5分
……………………………………5分
∴ …………………………………6分
…………………………………6分
(Ⅱ) 方法一
∵ ,
, ,∴
,∴ ,且
,且 ……7分
……7分
∴ ,从而
,从而 . …………………8分
. …………………8分
由(Ⅰ)知 ,
,
 ; ………………9分
; ………………9分
∴ . ………………………………10分
. ………………………………10分
又∵ ,∴
,∴ ,
又
,
又 ,∴
,∴ ……11分
……11分
综上可得  ………………………………12分
………………………………12分
方法二∵ ,
, ,∴
,∴ ,且
,且 …………7分
…………7分
∴ .
……………8分
.
……………8分
由(Ⅰ)知 ,
, .
…………9分
.
…………9分
∴ ……………10分
……………10分
∵ ,且注意到
,且注意到 ,
,
∴ ,又
,又 ,∴
,∴ ………………………11分
………………………11分
综上可得  …………………12分
…………………12分
(若用 ,又∵
,又∵ ∴
∴  ,
,
查看习题详情和答案>>