题目内容
抛掷一均匀的正方体玩具(各面分别标有数1、2、3、4、5、6),事件A表示“朝上一面的数是奇数”,事件B表示“朝上一面的数不超过下面给出两种不同的解法.
解法一:∵P(A)=![]() ,P(B)=
,P(B)=![]() ,
,
∴P(A+B)=P(A)+P(B)=1.
解法二:A+B这一事件包括4种结果,即出现1,2,3和5,
∴P(A+B)=![]() .
.
请你判断解法一和解法二的正误.
解:解法一是错误的,解法二是正确的. 错解的原因在于忽视了“事件和”概率公式应用的前提条件,由于“朝上一面的数是奇数”与“朝上一面的数不超过 而解法二中,将A+B分别出现“1、2、 ∴P(A+B)=P(C+D)=P(C)+P(D)=
![]() ,即解法二是正确的.
,即解法二是正确的. 练习册系列答案
练习册系列答案
京版教材配套资源英语新视野系列答案
自主学语文系列答案

每时每刻快乐优加系列答案
孟建平培优一号系列答案
孟建平毕业总复习系列答案
密解1对1系列答案
名师导练系列答案
名师讲堂单元同步学练测系列答案
名师面对面中考满分特训方案系列答案
相关题目
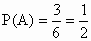 ,
,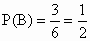 ,
,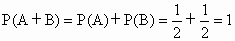 .
. .
.