摘要:(I) 以为坐标原点.直线.分别为轴.轴.过点垂直平面的直线为轴.建立空间直角坐标系如图.由题设条件.相关各点的坐标分别为
网址:http://m.1010jiajiao.com/timu_id_24136[举报]
已知F1、F2分别是椭圆 +
+ =1的左、右焦点,曲线C是坐标原点为顶点,以F2为焦点的抛物线,过点F1的直线l交曲线C于x轴上方两个不同点P、Q,点P关于x轴的对称点为M,设
=1的左、右焦点,曲线C是坐标原点为顶点,以F2为焦点的抛物线,过点F1的直线l交曲线C于x轴上方两个不同点P、Q,点P关于x轴的对称点为M,设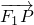 =
=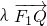
(I)若λ∈[2,4],求直线L的斜率k的取值范围;
(II)求证:直线MQ过定点.
查看习题详情和答案>>
已知F1、F2分别是椭圆
+
=1的左、右焦点,曲线C是坐标原点为顶点,以F2为焦点的抛物线,过点F1的直线l交曲线C于x轴上方两个不同点P、Q,点P关于x轴的对称点为M,设
=λ
(I)若λ∈[2,4],求直线L的斜率k的取值范围;
(II)求证:直线MQ过定点. 查看习题详情和答案>>
| x2 |
| 4 |
| y2 |
| 3 |
| F1P |
| F1Q |
(I)若λ∈[2,4],求直线L的斜率k的取值范围;
(II)求证:直线MQ过定点. 查看习题详情和答案>>
(本小题满分12分)
已知椭圆 的焦点在
的焦点在 轴上,离心率为
轴上,离心率为 ,对称轴为坐标轴,且经过点
,对称轴为坐标轴,且经过点 .
.
(I)求椭圆 的方程;
的方程;
(II)直线 与椭圆
与椭圆 相交于
相交于 、
、 两点,
两点,  为原点,在
为原点,在 、
、 上分别存在异于
上分别存在异于 点的点
点的点 、
、 ,使得
,使得 在以
在以 为直径的圆外,求直线斜率
为直径的圆外,求直线斜率 的取值范围.
的取值范围.
查看习题详情和答案>>
 的焦点在
的焦点在 轴上,离心率为
轴上,离心率为 ,对称轴为坐标轴,且经过点
,对称轴为坐标轴,且经过点 .
. 与椭圆
与椭圆 、
、 两点,
两点,  为原点,在
为原点,在 、
、 上分别存在异于
上分别存在异于 、
、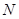 ,使得
,使得 为直径的圆外,求直线斜率
为直径的圆外,求直线斜率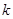 的取值范围.
的取值范围.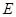 的焦点在
的焦点在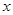 轴上,离心率为
轴上,离心率为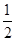 ,对称轴为坐标轴,且经过点
,对称轴为坐标轴,且经过点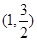 .
.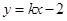 与椭圆
与椭圆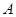 、
、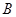 两点,
两点, 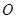 为原点,在
为原点,在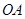 、
、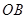 上分别存在异于
上分别存在异于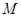 、
、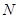 ,使得
,使得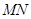 为直径的圆外,求直线斜率
为直径的圆外,求直线斜率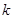 的取值范围.
的取值范围.