题目内容
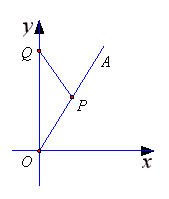
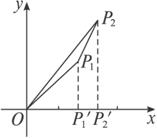
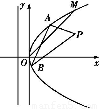
如下图所示,在直角坐标系![]() 中,射线
中,射线![]() 在第一象限,且与
在第一象限,且与![]() 轴的正半轴成定角
轴的正半轴成定角![]() ,动点
,动点![]() 在射线
在射线![]() 上运动,动点
上运动,动点![]() 在
在![]() 轴的正半轴上运动,
轴的正半轴上运动,![]() 的面积为
的面积为![]() .
.
(Ⅰ)求线段![]() 中点
中点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(Ⅱ)![]() 是曲线
是曲线![]() 上的动点,
上的动点, ![]() 到
到![]() 轴的距离之和为
轴的距离之和为![]() ,
,
设![]() 为
为![]() 到
到![]() 轴的距离之积.问:是否存在最大的常数
轴的距离之积.问:是否存在最大的常数![]() ,
,
使![]() 恒成立?若存在,求出这个
恒成立?若存在,求出这个![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1)![]() (
(![]() )(2)
)(2)![]()
解析:
(1)射线![]() .
.
设![]() (
(![]() ),
),
则![]() ,
,
又因为![]() 的面积为
的面积为![]() ,所以
,所以![]() ;
;
消去![]() 得点
得点![]() 的轨迹
的轨迹![]() 的方程为:
的方程为:![]() (
(![]() ).
).
(2)设![]() ,则
,则![]() ,
,
所以![]()
![]()
令![]() 则
则![]() ,所以有
,所以有![]() ,
,
则有:当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递减,
上单调递减,
所以当![]() 时,
时,![]() ,
,
所以存在最大的常数![]() 使
使![]() 恒成立.
恒成立.

练习册系列答案
相关题目
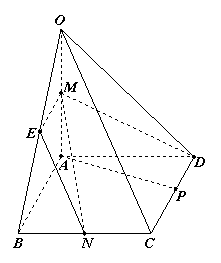
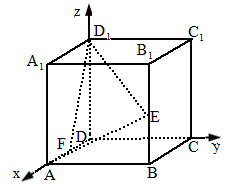
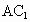 的棱长为1,E为
的棱长为1,E为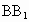 的中点,F为AD的中点,以DA、DC、
的中点,F为AD的中点,以DA、DC、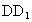 所在直线为x、y、z轴建立如下图所示空间直角坐标系,求平面
所在直线为x、y、z轴建立如下图所示空间直角坐标系,求平面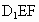 的法向量.
的法向量.
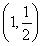
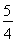
 时,拱顶离水面2米,水面宽4米,(1)建立如下图所示的直角坐标系,求抛物线的解析式。(2)水面下降1米后,水面宽是多少?
时,拱顶离水面2米,水面宽4米,(1)建立如下图所示的直角坐标系,求抛物线的解析式。(2)水面下降1米后,水面宽是多少?