网址:http://m.1010jiajiao.com/timu_id_23858[举报]
一、本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,有的小题只有一个选项是正确的,有的小题有多个选项是正确的。全部选对的得3分,选对但不全的得2分,有选错或不答的得0分。
1.AC 2.B 3.C 4.BD 5.D 6.B 7.AB 8.B 9.CD 10.ABD
二、本题共3小题,共14分。把答案填在题中的横线上。
11.ABD(3分) (注:选对但不全的得2分)
12.(1)F;F′ (3分) (2)不变 (2分)
13. ;(2分)
;(2分)  ;(2分) mg
;(2分) mg (2分)
(2分)
(注:用相邻两段位移表达出来,只要表达正确的不扣分)
三、本题包括7小题,共56分。解答应写出必要的文字说明,方程式和重要的演算步骤。只写出最后答案的不能得分,有数值计算的题的答案必须明确写出数值和单位。
14.(7分)
解:(1)设斜面对箱子的支持力为N,箱了上滑的加速度为a。根据牛顿第二定律,得平行斜面方向,F-mgsin37°-μN=ma, …………1分
垂直斜面方向,N=mgcos37°, …………1分
解得箱子的加速度a= (sin37°+μcos37°)=2.4m/s2 …………2分
(sin37°+μcos37°)=2.4m/s2 …………2分
(2)设箱子滑到斜面顶端的速度v,由运动学公式,
v2=2as, …………2分
解得 v= 。 …………1分
。 …………1分
15.(7分)
解:(1)设塔顶距地面的高度为h,根据自由落体运动公式,得
h= gt2=80m。 …………2分
gt2=80m。 …………2分
(2)设石块落地时的速度为v,根据匀变速运动规律,v=gt。 …………2分
设石块落地时重力做功的功率为P,则P=mgv=mg2t=2.0×103W 。…………3分
16.(8分)
解:(1)滑块B沿轨道下滑过程中,机械能守恒,设滑块B与A碰撞前瞬间的速度为v1,则 mgR= 。 …………1分
。 …………1分
滑块B与滑块A碰撞过程沿水平方向动量守恒,设碰撞后的速度为v2,则
mv1=2mv2 。 …………1分
设碰撞后滑块C受到轨道的支持力为N,根据牛顿第二定律,对滑块C在轨道最低点有 N-2mg=2mv /R ,…………1分
/R ,…………1分
联立各式可解得, N=3mg。 …………1分
根据牛顿第三定律可知,滑块C对轨道末端的压力大小为N′=3mg。…………1分
(2)滑块C离开轨道末端做平抛运动,设运动时间t,根据自由落体公式,
h= gt2 。…………1分
gt2 。…………1分
滑块C落地点与轨道末端的水平距离为s=v2t ,…………1分
联立以上各式解得s= 。 …………1分
。 …………1分
17.(8分)
解:(1)飞船在圆轨道上做匀速圆周运动,运行的周期 T= 。 …………1分
。 …………1分
设飞船做圆运动距地面的高度为h,飞船受到地球的万有引力提供了飞船的向心力,根据万有引力定律和牛顿第二定律,得
 。 …………2分
。 …………2分
而地球表面上的物体受到的万有引力近似等于物体的重力,即
 =mg, …………1分
=mg, …………1分
联立以上各式,解得 h= -R。 …………1分
-R。 …………1分
(2)飞船运动的圆轨道的周长 s=2π(R+h), …………1分
动行的速度 v= =
= , …………1分
, …………1分
解得 v= 。 …………1分
。 …………1分
18.(8分)
解:(1)重锤在竖直平面内做匀速圆周运动,当重锤运动通过最高点时,打夯机底座受连接杆竖直向上的作用力达到最大。此时重锤所受的重力mg和连接杆对重锤向下的拉力T1提供重锤的向心力,根牛顿第二定律
T1+mg=mw2R。 …………1分
连接杆对打夯机底座向上的拉力 T1′=T1。 …………1分
当T′=Mg时,打夯机底座刚好离开地面, …………1分
解得 ω= 。 …………1分
。 …………1分
(2)当重锤通过最低位置时,重锤所受的重力mg和连接杆的拉力T2的合力提供重锤的向心力,根据牛顿第二定有: T2-mg=mw2R。…………1分
连接杆对打夯机底座的作用力T2′的方向向下,且T2′=T2。
设打夯机受到地面的支持力N,根据牛顿第二定律,
N=Mg+T2’ ,…………1分
联立以上各式解得 N=2(M+m)g 。…………1分
根据牛顿第三定律,打夯机对地面压力的大小N′=N=2(M+m)g。…………1分
19.(9分)
解:(1)设运动员在空中飞行时间为t,运动员在竖直方向做自由落体运动,得
ssin37°= gt2,
gt2,
解得: t= =1.2s。…………2分
=1.2s。…………2分
(2)设运动员离开O点的速度为v0,运动员在水平方向做匀速直线运动,即
scos37°=v0t,
解得: v0= =8.0m/s。…………2分
=8.0m/s。…………2分
(3)运动员落在A点时沿竖直向下的速度vy的大小为
vy=gt=12m/s …………1分,
沿水平方向的速度vx的大小为 vx=8.0m/s。
因此,运动员垂直于斜面向下的速度vN为
vN=vycos37°-vxsin37°=4.8m/s。 …………1分
设运动员在缓冲的过程中受到斜面的弹力为N,根据动量定理
(N-mgcos37°)t=mvN,…………1分
解得: N=mgcos37°+ =880N。…………1分
=880N。…………1分
20.(9分)
解:(1)设物块滑上小车后经过时间t1速度减为零,根据动量定理
μmgt1=mv,
解得: t1= =0.5s 。…………1分
=0.5s 。…………1分
(2)物块滑上小车后,做加速度为am的匀变速运动,根牛顿第二定律
μmg=mam,
解得: am=μg=2.0m/s2。
小车做加速度为aM的匀加速运动,根据牛顿第二定律
F-μmg=MaM,
解得: aM= =0.5m/s2。…………1分
=0.5m/s2。…………1分
设物块向左滑动的位移为s1,根据运动学公式
s1=v0t1- amt
amt =0.25m,
=0.25m,
当滑块的速度为零时,小车的速度V1为
V1=V0+amt1=1.75m/s。
设物块向右滑动经过时间t2相对小车静止,此后物块与小车有共同速度V,根据运动学公式,有 V=V1+aMt2=amt2,
解得: t2= s。 …………1分
s。 …………1分
滑块在时间t2内的位移为s2= ams
ams =
= m≈1.36m。(方向向右) …………1分
m≈1.36m。(方向向右) …………1分
因此,滑块在小车上滑动的过程中相对地面的位移为
s=s2-s1= m≈1.11m,方向向右。…………1分
m≈1.11m,方向向右。…………1分
(3)由(2)的结果,物块与小车的共同速度
V= m/s,
m/s,
因此,物块在小车上相对小车滑动的过程中,系统的机械能增加量ΔE为
ΔE= (m+M)V2-
(m+M)V2- mv
mv -
- MV
MV ≈17.2J。…………2分
≈17.2J。…………2分
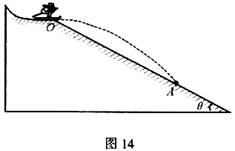 高台滑雪运动员经过一段滑行后从斜坡上的O点水平飞出,斜坡与水平面的夹角θ=37°,运动员连同滑雪板的总质量m=50kg,他落到了斜坡上的A点,A点与O点的距离s=12m,如图14所示。忽略斜坡的摩擦和空气阻力的影响,重力加速度g=10m/s2。
高台滑雪运动员经过一段滑行后从斜坡上的O点水平飞出,斜坡与水平面的夹角θ=37°,运动员连同滑雪板的总质量m=50kg,他落到了斜坡上的A点,A点与O点的距离s=12m,如图14所示。忽略斜坡的摩擦和空气阻力的影响,重力加速度g=10m/s2。
(sin37°=0.60;cos37°=0.80)
(1)运动员在空中飞行了多长时间?
(2)求运动员离开O点时的速度大小。
(3)运动员落到斜坡上顺势屈腿以缓冲,使他垂直于斜坡的速度在t=0.50s的时间内减小为零,设缓冲阶段斜坡对运动员的弹力可以看作恒力,求此弹力的大小。
查看习题详情和答案>>
(sin37°=0.60;cos37°=0.80)
(1)运动员在空中飞行了多长时间?
(2)求运动员离开O点时的速度大小。
(3)运动员落到斜坡上顺势屈腿以缓冲,使他垂直于斜坡的速度在t=0.50s的时间内减小为零,设缓冲阶段斜坡对运动员的弹力可以看作恒力,求此弹力的大小。
高台滑雪运动员经过一段滑行后从斜坡上O点水平飞出,斜坡与水平面的夹角![]() =37°,运动员连同滑雪板的总质量m=50 kg,他落到了斜坡上的A点,A点与O点的距离s=12 m,如图所示.忽略斜坡的摩擦和空气阻力的影响,重力加速度g=10 m/s2.(sin37°=0.60;cos37°=0.80)
=37°,运动员连同滑雪板的总质量m=50 kg,他落到了斜坡上的A点,A点与O点的距离s=12 m,如图所示.忽略斜坡的摩擦和空气阻力的影响,重力加速度g=10 m/s2.(sin37°=0.60;cos37°=0.80)
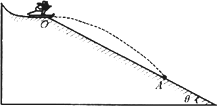
(1)运动员在空中飞行了多长时间?
(2)求运动员离开O点时的速度大小.