网址:http://m.1010jiajiao.com/timu_id_23836[举报]
一、本题共10小题,每小题3分,共30分。在每小题给出的四个选项中,有的小题只有一个选项是正确的,有的小题有多个选项是正确的。全部选对的得3分,选对但不全的得2分,有选错或不答的得0分。
1.AC 2.B 3.C 4.BD 5.D 6.B 7.AB 8.B 9.CD 10.ABD
二、本题共3小题,共14分。把答案填在题中的横线上。
11.ABD(3分) (注:选对但不全的得2分)
12.(1)F;F′ (3分) (2)不变 (2分)
13. ;(2分)
;(2分)  ;(2分) mg
;(2分) mg (2分)
(2分)
(注:用相邻两段位移表达出来,只要表达正确的不扣分)
三、本题包括7小题,共56分。解答应写出必要的文字说明,方程式和重要的演算步骤。只写出最后答案的不能得分,有数值计算的题的答案必须明确写出数值和单位。
14.(7分)
解:(1)设斜面对箱子的支持力为N,箱了上滑的加速度为a。根据牛顿第二定律,得平行斜面方向,F-mgsin37°-μN=ma, …………1分
垂直斜面方向,N=mgcos37°, …………1分
解得箱子的加速度a= (sin37°+μcos37°)=2.4m/s2 …………2分
(sin37°+μcos37°)=2.4m/s2 …………2分
(2)设箱子滑到斜面顶端的速度v,由运动学公式,
v2=2as, …………2分
解得 v= 。 …………1分
。 …………1分
15.(7分)
解:(1)设塔顶距地面的高度为h,根据自由落体运动公式,得
h= gt2=80m。 …………2分
gt2=80m。 …………2分
(2)设石块落地时的速度为v,根据匀变速运动规律,v=gt。 …………2分
设石块落地时重力做功的功率为P,则P=mgv=mg2t=2.0×103W 。…………3分
16.(8分)
解:(1)滑块B沿轨道下滑过程中,机械能守恒,设滑块B与A碰撞前瞬间的速度为v1,则 mgR= 。 …………1分
。 …………1分
滑块B与滑块A碰撞过程沿水平方向动量守恒,设碰撞后的速度为v2,则
mv1=2mv2 。 …………1分
设碰撞后滑块C受到轨道的支持力为N,根据牛顿第二定律,对滑块C在轨道最低点有 N-2mg=2mv /R ,…………1分
/R ,…………1分
联立各式可解得, N=3mg。 …………1分
根据牛顿第三定律可知,滑块C对轨道末端的压力大小为N′=3mg。…………1分
(2)滑块C离开轨道末端做平抛运动,设运动时间t,根据自由落体公式,
h= gt2 。…………1分
gt2 。…………1分
滑块C落地点与轨道末端的水平距离为s=v2t ,…………1分
联立以上各式解得s= 。 …………1分
。 …………1分
17.(8分)
解:(1)飞船在圆轨道上做匀速圆周运动,运行的周期 T= 。 …………1分
。 …………1分
设飞船做圆运动距地面的高度为h,飞船受到地球的万有引力提供了飞船的向心力,根据万有引力定律和牛顿第二定律,得
 。 …………2分
。 …………2分
而地球表面上的物体受到的万有引力近似等于物体的重力,即
 =mg, …………1分
=mg, …………1分
联立以上各式,解得 h= -R。 …………1分
-R。 …………1分
(2)飞船运动的圆轨道的周长 s=2π(R+h), …………1分
动行的速度 v= =
= , …………1分
, …………1分
解得 v= 。 …………1分
。 …………1分
18.(8分)
解:(1)重锤在竖直平面内做匀速圆周运动,当重锤运动通过最高点时,打夯机底座受连接杆竖直向上的作用力达到最大。此时重锤所受的重力mg和连接杆对重锤向下的拉力T1提供重锤的向心力,根牛顿第二定律
T1+mg=mw2R。 …………1分
连接杆对打夯机底座向上的拉力 T1′=T1。 …………1分
当T′=Mg时,打夯机底座刚好离开地面, …………1分
解得 ω= 。 …………1分
。 …………1分
(2)当重锤通过最低位置时,重锤所受的重力mg和连接杆的拉力T2的合力提供重锤的向心力,根据牛顿第二定有: T2-mg=mw2R。…………1分
连接杆对打夯机底座的作用力T2′的方向向下,且T2′=T2。
设打夯机受到地面的支持力N,根据牛顿第二定律,
N=Mg+T2’ ,…………1分
联立以上各式解得 N=2(M+m)g 。…………1分
根据牛顿第三定律,打夯机对地面压力的大小N′=N=2(M+m)g。…………1分
19.(9分)
解:(1)设运动员在空中飞行时间为t,运动员在竖直方向做自由落体运动,得
ssin37°= gt2,
gt2,
解得: t= =1.2s。…………2分
=1.2s。…………2分
(2)设运动员离开O点的速度为v0,运动员在水平方向做匀速直线运动,即
scos37°=v0t,
解得: v0= =8.0m/s。…………2分
=8.0m/s。…………2分
(3)运动员落在A点时沿竖直向下的速度vy的大小为
vy=gt=12m/s …………1分,
沿水平方向的速度vx的大小为 vx=8.0m/s。
因此,运动员垂直于斜面向下的速度vN为
vN=vycos37°-vxsin37°=4.8m/s。 …………1分
设运动员在缓冲的过程中受到斜面的弹力为N,根据动量定理
(N-mgcos37°)t=mvN,…………1分
解得: N=mgcos37°+ =880N。…………1分
=880N。…………1分
20.(9分)
解:(1)设物块滑上小车后经过时间t1速度减为零,根据动量定理
μmgt1=mv,
解得: t1= =0.5s 。…………1分
=0.5s 。…………1分
(2)物块滑上小车后,做加速度为am的匀变速运动,根牛顿第二定律
μmg=mam,
解得: am=μg=2.0m/s2。
小车做加速度为aM的匀加速运动,根据牛顿第二定律
F-μmg=MaM,
解得: aM= =0.5m/s2。…………1分
=0.5m/s2。…………1分
设物块向左滑动的位移为s1,根据运动学公式
s1=v0t1- amt
amt =0.25m,
=0.25m,
当滑块的速度为零时,小车的速度V1为
V1=V0+amt1=1.75m/s。
设物块向右滑动经过时间t2相对小车静止,此后物块与小车有共同速度V,根据运动学公式,有 V=V1+aMt2=amt2,
解得: t2= s。 …………1分
s。 …………1分
滑块在时间t2内的位移为s2= ams
ams =
= m≈1.36m。(方向向右) …………1分
m≈1.36m。(方向向右) …………1分
因此,滑块在小车上滑动的过程中相对地面的位移为
s=s2-s1= m≈1.11m,方向向右。…………1分
m≈1.11m,方向向右。…………1分
(3)由(2)的结果,物块与小车的共同速度
V= m/s,
m/s,
因此,物块在小车上相对小车滑动的过程中,系统的机械能增加量ΔE为
ΔE= (m+M)V2-
(m+M)V2- mv
mv -
- MV
MV ≈17.2J。…………2分
≈17.2J。…………2分
(1)下列说法正确的是
A.为平衡小车与水平木板之间摩擦力,应将木板不带滑轮的一端适当垫高,在挂小盘(及砝码)的情况下使小车恰好做匀速运动
B.每次改变小车质量时,应重新平衡摩擦力
C.本实验中要满足m2应远小于m1的条件
D.在用图象探究加速度与质量关系时,应作a-m1图象
(2)实验中,得到一条打点的纸带,如图2所示,已知相邻计数点间的时间间隔为T,且间距x1、x2、x3、x4、x5、x6已量出,则计算小车加速度的表达式为a=
| x4+x5+x6-x1-x2-x3 |
| 9T2 |
| x4+x5+x6-x1-x2-x3 |
| 9T2 |
(3)某同学在平衡好摩擦力后,保持小车质量不变的情况下,通过多次改变砝码重力,作出小车加速度a与砝码重力F的图象如图3所示,若牛顿第二定律成立,重力加速度g=10m/s2,则小车的质量为
(4)如果砝码的重力越来越大时,小车的加速度不能无限制地增加,会趋近于某一极限值,此极限值为

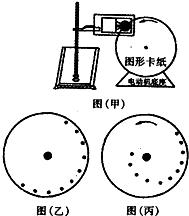 如图甲所示为测量电动机转动角速度的实验装置,半径不大的圆形卡纸固定在电动机转轴上,在电动机的带动下匀速转动.在圆形卡纸旁边垂直安装一个改装了的电火花计时器.
如图甲所示为测量电动机转动角速度的实验装置,半径不大的圆形卡纸固定在电动机转轴上,在电动机的带动下匀速转动.在圆形卡纸旁边垂直安装一个改装了的电火花计时器.(1)请将下列实验步骤按先后顺序排序:
①使电火花计时器与圆形卡纸保持良好接触
②接通电火花计时器的电源,使它工作起来
③启动电动机,使圆形卡纸转动起来
④关闭电动机,拆除电火花计时器,研究卡纸上留下的一段痕迹(如图乙所示),写出角速度ω的表达式,代入数据,得出ω的测量值
(2)要得到角速度ω的测量值,还缺少一种必要的测量工具,它是
A.秒表 B.毫米刻度尺 C.圆规 D.量角器
(3)写出ω的表达式,并指出表达式中各个物理的意义:
(4)为了避免在卡纸连续转动的过程中出现打点重叠,在电火花计时器与盘面保持良好接触的同时,可以缓慢地将电火花计时器沿圆形卡纸半径方向向卡纸中心移动.则卡纸上打下的点分布曲线将不是一个圆,而是类似一种螺旋线(如图丙所示).这样做测量结果将

(1)首先对多用电表进行机械调零,然后将红、黑表笔正确插入插孔后,选用×100档进行测量,在测量前要进行的操作步骤为:
(2)将多用电表的红表笔与二极管的A端、黑表笔与二极管的B端相连时,表的指针偏转角度很大;调换表笔的连接后,表的指针偏转角度很小,由上述测量可知该二极管的正极为
(3)用一个满偏电流为3mA的电流表,改装成的欧姆表,调整零点以后,测量500Ω的标准电阻时,指针恰好指在表盘的正中央,测量某未知电阻时,指针指在1mA处,则被测电阻的阻值为
(4)用多用电表进行粗测:多用电表电阻档有3种倍率,分别是×100Ω、×10Ω和×1Ω.该同学选择×10Ω倍率,用正确的操作方法测量时,发现指针偏转角度太小.为了较准确地进行测量,应重新选择
如图16所示为某种弹射装置的示意图,光滑的水平导轨MN右端N处与水平传送带理想连接,传送带长度 L = 4.0 m,皮带轮沿顺时针方向转动,带动皮带以恒定速率v = 3.0 m/s 匀速传动.三个质量均为m = 1.0 kg 的滑块A、B、C置于水平导轨上,开始时滑块B、C之间用细绳相连,其间有一压缩的轻弹簧,处于静止状态.滑块A以初速度v0 = 2.0 m/s 沿B、C连线方向向B运动,A与B碰撞后粘合在一起,碰撞时间极短.连接B、C的细绳受扰动而突然断开,弹簧伸展,从而使C与A、B分离.滑块C脱离弹簧后以速度vC = 2.0 m/s 滑上传送带,并从右端滑出落至地面上的P点.
已知滑块C与传送带之间的动摩擦因数μ = 0.20,重力加速度g取10 m/s2.求:
(1)滑块C从传送带右端滑出时的速度大小;
(2)滑块B、C用细绳相连时弹簧的弹性势能Ep;
(3)若每次实验开始时弹簧的压缩情况相同,要使滑块C总能落至P点,则滑块A与滑块B碰撞前速度的最大值Vm是多少?

如图16所示为某种弹射装置的示意图,光滑的水平导轨MN右端N处与水平传送带理想连接,传送带长度 L = 4.0 m,皮带轮沿顺时针方向转动,带动皮带以恒定速率v = 3.0 m/s 匀速传动.三个质量均为m = 1.0 kg 的滑块A、B、C置于水平导轨上,开始时滑块B、C之间用细绳相连,其间有一压缩的轻弹簧,处于静止状态.滑块A以初速度v0 =2.0 m/s 沿B、C连线方向向B运动,A与B碰撞后粘合在一起,碰撞时间极短.连接B、C的细绳受扰动而突然断开,弹簧伸展,从而使C与A、B分离.滑块C脱离弹簧后以速度vC =2.0 m/s 滑上传送带,并从右端滑出落至地面上的P点.
已知滑块C与传送带之间的动摩擦因数μ = 0.20,重力加速度g取10 m/s2.求:
(1)滑块C从传送带右端滑出时的速度大小;
(2)滑块B、C用细绳相连时弹簧的弹性势能Ep;
(3)若每次实验开始时弹簧的压缩情况相同,要使滑块C总能落至P点,则滑块A与滑块B碰撞前速度的最大值Vm是多少?
查看习题详情和答案>>