摘要：曲线C是由点M轨迹及其关于边AB对称的曲线组成.F(0, ),过点F的直线交曲线C于P.Q两点.且.求的范围.
网址：http://m.1010jiajiao.com/timu_id_23376[举报]
已知曲线C：x2+
=1，直线l：kx-y-k=0，O为坐标原点．
（1）讨论曲线C所表示的轨迹形状；
（2）当k=1时，直线l与曲线C相交于两点M，N，若|MN|=
，求曲线C的方程；
（3）当a=-1时，直线l与曲线C相交于两点M，N，试问在曲线C上是否存在点Q，使得
+
=λ
？若存在，求实数λ的取值范围；若不存在，请说明理由．
查看习题详情和答案>>
| y2 |
| a |
（1）讨论曲线C所表示的轨迹形状；
（2）当k=1时，直线l与曲线C相交于两点M，N，若|MN|=
| 2 |
（3）当a=-1时，直线l与曲线C相交于两点M，N，试问在曲线C上是否存在点Q，使得
| OM |
| ON |
| OQ |
动点M（x，y）到定点F（-1，0）的距离与到y轴的距离之差为1．
（I）求动点M的轨迹C的方程；
（II）过点Q（-3，0）的直线l与曲线C交于A、B两点，问直线x=3上是否存在点P，使得△PAB是等边三角形？若存在，求出所有的点P；若不存在，请说明理由．
查看习题详情和答案>>
（I）求动点M的轨迹C的方程；
（II）过点Q（-3，0）的直线l与曲线C交于A、B两点，问直线x=3上是否存在点P，使得△PAB是等边三角形？若存在，求出所有的点P；若不存在，请说明理由．
已知曲线C：
+x2=1；
（1）由曲线C上任一点E向x轴作垂线，垂足为F，点P在
上，且
=-
．问：点P的轨迹可能是圆吗？请说明理由；
（2）如果直线l的斜率为
，且过点M（0，-2），直线l交曲线C于A，B两点，又
•
=-
，求曲线C的方程．
查看习题详情和答案>>
| y2 |
| m |
（1）由曲线C上任一点E向x轴作垂线，垂足为F，点P在
| EF |
| EP |
| 1 |
| 3 |
| PF |
（2）如果直线l的斜率为
| 2 |
| MA |
| MB |
| 9 |
| 2 |
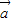=（x-2，y），
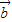=（x+2，y），且|a|+|b|=8，
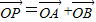（O为坐标原点），是否存在直线l，使得四边形OAPB为矩形，若存在，求出直线l的方程，若不存在，请说明理由．
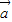=（x-2，y），
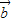=（x+2，y），且|a|+|b|=8，
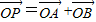（O为坐标原点），是否存在直线l，使得四边形OAPB为矩形，若存在，求出直线l的方程，若不存在，请说明理由．