网址:http://m.1010jiajiao.com/timu_id_23279[举报]
1.D 2.C 3.C 4.A 5.A 6.D 7.C 8.D 9.A 10.C
11.  12.
8 13.
12.
8 13.  14.
14.  15. 2
15. 2
16.依题意,即 ,由函数为奇函数,
,由函数为奇函数,
∴对于定义域内的任意x有 ,即
,即
∴ ,即
,即 ,
,
由
又

且
解得
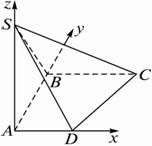
17.(1)如图建立空间直角坐标系,设 ,且
,且
 由
由

∴

∴
∴SC与AD所成的角为
18.(1)最后甲获胜的概率为P1,乙获胜的概率为P2,则 ,∴甲、乙两队各自获胜的概率分
,∴甲、乙两队各自获胜的概率分
(2)乙队第五局必须获胜,前四局为独立重复实验,乙队3∶2获胜的概率为P3,则 ,∴乙队以3∶2获胜的概率为
,∴乙队以3∶2获胜的概率为
19.(1)联立两个方程,从中消去y得
∴
注意到a>b>c, a+b+c=0,∴a>0, c<0, ∴△>0, 故两条曲线必交于两个不同的交点A、B;
(2)设 的两个根为x1、x2,则AB在x轴上的射影的长
的两个根为x1、x2,则AB在x轴上的射影的长

由 ,由此可得
,由此可得
20.(1)设{an}的公差为d,则65=
∴
(2)设函数
故当x=e时 ,且当0<x<e时
,且当0<x<e时 ,当x>e时
,当x>e时 ,
,
∴函数 在区间(0,e)内单调递增,而在区间
在区间(0,e)内单调递增,而在区间 上单调递减,由
上单调递减,由 及函数
及函数 单调递增可知函数
单调递增可知函数 与f(x)有相同的单调性,即
与f(x)有相同的单调性,即 在区间(0,e)内单调递增,而在区间
在区间(0,e)内单调递增,而在区间 上单调递减,
上单调递减,
注意到 ,由2<e<3知数列{bn}的最大项是第2项,这一项是
,由2<e<3知数列{bn}的最大项是第2项,这一项是 ;
;
(3)在数列{cn}不存在这样的项使得它们按原顺序成等比数列. 事实上由
∴
有 . 综合知即无法找到这样的一些连续的项使其成等比数列.
. 综合知即无法找到这样的一些连续的项使其成等比数列.
21.(1)若直线l与x轴不垂直,设其方程为 ,l与抛物线
,l与抛物线 的交点坐标分别为
的交点坐标分别为 、
、 ,由
,由 得
得 ,即
,即 ,
,
则
 又由
又由 得
得 .
.
则 即
即 ,则直线l的方程为
,则直线l的方程为 ,
,
则直线l过定点(2,0).
若直线l与x轴垂直,易得 l的方程为x=2,
l的方程为x=2,
则l也过定点(2,0). 综上,直线l恒过定点(2,0).
(2)由(1)得 ,可得
,可得 解得k的取值范围是
解得k的取值范围是
(3)假定 ,则有
,则有 ,如图,即
,如图,即
由(1)得 . 由定义得
. 由定义得 从而有
从而有

 均代入(*)得
均代入(*)得
 ,即
,即 这与
这与 相矛盾.
相矛盾.
经检验,当 轴时,
轴时, . 故
. 故
 已知△ABC中∠ACB=90°,SA⊥面ABC,AD⊥SC.
已知△ABC中∠ACB=90°,SA⊥面ABC,AD⊥SC.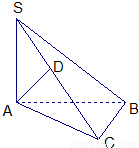
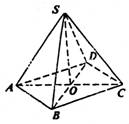 菱形ABCD的边长为
菱形ABCD的边长为