题目内容
如图所示,ABCD是直角梯形,∠ABC=90°,SA⊥面ABCD,SA=AB=BC=1,AD=(1)求面SCD与面SBA所成的二面角的大小;
(2)求SC与平面ABCD所成的角.
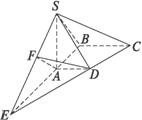
解:(1)延长CD,BA交于E点,易知SE为平面SCD与SBA的交线.
过点A作AF⊥SE于点F,连结DF,

∵SA⊥平面ABCD,
∴SA⊥AD.
又AD⊥BE,∴AD⊥平面SAB.则易知∠AFD为二面角B-SE-C的平面角,即∠AFD是平面SCD与平面SBA所成的角.
在△SAE中,易求SA=AE,且AF=![]() SA=
SA=![]() .
.
∴tan∠AFD=![]() ,即∠AFD=arctan
,即∠AFD=arctan![]() .
.
(2)易知∠SCA为所求角,且AC=![]() ,SA=1,tan∠SCA=
,SA=1,tan∠SCA=![]() =
=![]() ,∴∠SCA=arctan
,∴∠SCA=arctan![]() .
.

练习册系列答案
相关题目