摘要:所以. 又.所以() .因为.所以 即.又所以是等腰直角三角形.()
网址:http://m.1010jiajiao.com/timu_id_215214[举报]
解:因为∠B=∠C
所以AB∥CD(________)
又因为AB∥EF
所以EF∥CD(________)
所以∠BGF=∠C(________)
(2)如图,AD⊥BC于D,EG⊥BC于G,∠E=∠3
试说明:AD平分∠BAC
解:因为AD⊥BC,EG⊥BC
所以AD∥EG(________)
所以∠1=∠E(________)
∠2=∠3(________ )
又因为∠3=∠E
所以∠1=∠2
所以AD平分∠BAC(________)
(3)如图,EF∥AD,∠1=∠2,∠BAC=70°.求∠AGD的度数.
解:因为EF∥AD,
所以∠2=________ (________)
又因为∠1=∠2
所以∠1=∠3 (________)
所以AB∥________ (________)
所以∠BAC+________=180°(________)
因为∠BAC=70°
所以∠AGD=________.
查看习题详情和答案>>
如图8所示,因为AC平分∠DAB(已知),所以∠1=∠3(__________________).
又因为∠1=∠2(已知),所以∠2=∠3(_____________________________).
所以DC∥AB(___________________________________).
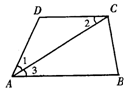
如图9所示,C、D、E在一条直线上.
因为∠1=130°(已知),
所以∠2=50°(_________).
又因为∠A=50°(已知),
所以∠2=∠A(_________).
所以AB∥CD(____________).

(2006•汉川市)某地为促进特种水产养殖业的发展,决定对甲鱼和黄鳝的养殖提供政府补贴.该地某农户在改建的10个1亩大小的水池里分别养殖甲鱼和黄鳝,因资金有限,投入不能超过14万元,并希望获得不低于10.8万元的收益,相关信息如下表所示:(收益=毛利润-成本+政府补贴)
(1)根据以上信息,该农户可以怎样安排养殖?
(2)应怎样安排养殖,可获得最大收益?
(3)据市场调查,在养殖成本不变的情况下,黄鳝的毛利润相对稳定,而每亩甲鱼的毛利润将减少m万元.问该农户又该如何安排养殖,才能获得最大收益?
查看习题详情和答案>>
| 养殖种类 | 成本(万元/亩) | 毛利润(万元/亩) | 政府补贴(万元/亩) |
| 甲鱼 | 1.5 | 2.5 | 0.2 |
| 黄鳝 | 1 | 1.8 | 0.1 |
(2)应怎样安排养殖,可获得最大收益?
(3)据市场调查,在养殖成本不变的情况下,黄鳝的毛利润相对稳定,而每亩甲鱼的毛利润将减少m万元.问该农户又该如何安排养殖,才能获得最大收益?
查看习题详情和答案>>
动手做一做
(1)如图1,因为∠1=∠2,(已知)∠2=∠3,(
(2)如图2,因为∠1=110°(已知)∠1+∠2=180°,(
(3)如图3:∵∠2=∠3 (已知∴
∴
(4)如图4,已知:∠1=120°,∠C=60°.说明AB∥CD的理由.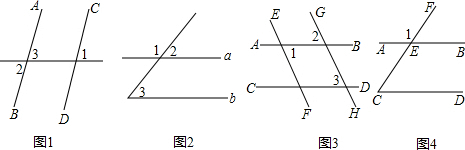
查看习题详情和答案>>
(1)如图1,因为∠1=∠2,(已知)∠2=∠3,(
对顶角相等
对顶角相等
)所以∠1=∠3,(等量代换
等量代换
)所以AB∥CD.(同位角相等,两直线平行
同位角相等,两直线平行
)(2)如图2,因为∠1=110°(已知)∠1+∠2=180°,(
邻补角定义
邻补角定义
)所以∠2=70°
70°
又因为∠3=70°,(已知所以∠2=∠3,所以a∥b.(同位角相等,两直线平行
同位角相等,两直线平行
)(3)如图3:∵∠2=∠3 (已知∴
AB
AB
∥CD
CD
(同位角相等,两直线平行
同位角相等,两直线平行
又∵EF∥GH (已知)∴
∠1
∠1
=∠2
∠2
(两直线平行,内错角相等
两直线平行,内错角相等
)∴∠1=∠3(4)如图4,已知:∠1=120°,∠C=60°.说明AB∥CD的理由.
