题目内容
动手做一做
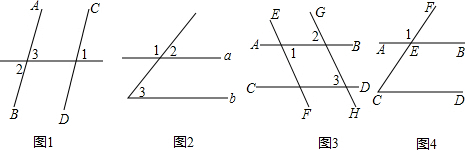
(1)如图1,因为∠1=∠2,(已知)∠2=∠3,(
(2)如图2,因为∠1=110°(已知)∠1+∠2=180°,(
(3)如图3:∵∠2=∠3 (已知∴
∴
(4)如图4,已知:∠1=120°,∠C=60°.说明AB∥CD的理由.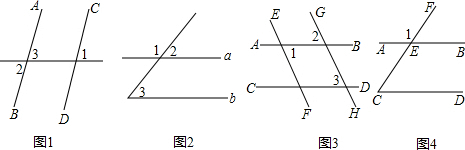
(1)如图1,因为∠1=∠2,(已知)∠2=∠3,(
对顶角相等
对顶角相等
)所以∠1=∠3,(等量代换
等量代换
)所以AB∥CD.(同位角相等,两直线平行
同位角相等,两直线平行
)(2)如图2,因为∠1=110°(已知)∠1+∠2=180°,(
邻补角定义
邻补角定义
)所以∠2=70°
70°
又因为∠3=70°,(已知所以∠2=∠3,所以a∥b.(同位角相等,两直线平行
同位角相等,两直线平行
)(3)如图3:∵∠2=∠3 (已知∴
AB
AB
∥CD
CD
(同位角相等,两直线平行
同位角相等,两直线平行
又∵EF∥GH (已知)∴
∠1
∠1
=∠2
∠2
(两直线平行,内错角相等
两直线平行,内错角相等
)∴∠1=∠3(4)如图4,已知:∠1=120°,∠C=60°.说明AB∥CD的理由.

分析:利用平行线的判定与性质即可得到结果.
解答:解:(1)如图1,因为∠1=∠2,(已知)∠2=∠3,(对顶角相等),
所以∠1=∠3,(等量代换),
所以AB∥CD.(同位角相等,两直线平行);
(2)如图2,因为∠1=110°(已知),∠1+∠2=180°,(邻补角定义)
所以∠2=70°,又因为∠3=70°,(已知),
所以∠2=∠3,所以a∥b.(同位角相等,两直线平行);
(3)如图3:∵∠2=∠3 (已知),
∴AB∥CD (同位角相等,两直线平行),
又∵EF∥GH(已知)
∴∠1=∠2(两直线平行,内错角相等),
∴∠1=∠3;
(4)∵∠1=120°,∠1=∠BEC,
∴∠BEC=120°,
∵∠C=60°,
∴∠BEC+∠C=180°,
∴AB∥CD.
故答案为:(1)对顶角相等;等量代换;同位角相等,两直线平行;(2)邻补角定义;70°;同位角相等,两直线平行;(3)同位角相等,两直线平行;∠1;∠2;两直线平行,内错角相等.
所以∠1=∠3,(等量代换),
所以AB∥CD.(同位角相等,两直线平行);
(2)如图2,因为∠1=110°(已知),∠1+∠2=180°,(邻补角定义)
所以∠2=70°,又因为∠3=70°,(已知),
所以∠2=∠3,所以a∥b.(同位角相等,两直线平行);
(3)如图3:∵∠2=∠3 (已知),
∴AB∥CD (同位角相等,两直线平行),
又∵EF∥GH(已知)
∴∠1=∠2(两直线平行,内错角相等),
∴∠1=∠3;
(4)∵∠1=120°,∠1=∠BEC,
∴∠BEC=120°,
∵∠C=60°,
∴∠BEC+∠C=180°,
∴AB∥CD.
故答案为:(1)对顶角相等;等量代换;同位角相等,两直线平行;(2)邻补角定义;70°;同位角相等,两直线平行;(3)同位角相等,两直线平行;∠1;∠2;两直线平行,内错角相等.
点评:此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目