摘要：(1)若在区间上为减函数.求实数的取值范围.
网址：http://m.1010jiajiao.com/timu_id_21431[举报]
在区间
上为减函数，求实数
的取值范围；
在函数y=f（x）在区间（0，+∞）内可导．导函数f′（x）是减函数，且f′（x）＞0，x0∈（0，+∞）．g（x）=kx+m是y=f（x）在点（x0，f（x0））处的切线方程．
（1）用x0，f（x0），f′（x0）表示m；
（2）证明：当x∈（0，+∞）时，g（x）≥f（x）；
（3）若关于x的不等式x2+1≥ax+b≥
x
在（0，+∞）上恒成立，其中a，b为实数，求b的取值范围及a，b所满足的关系．
查看习题详情和答案>>
（1）用x0，f（x0），f′（x0）表示m；
（2）证明：当x∈（0，+∞）时，g（x）≥f（x）；
（3）若关于x的不等式x2+1≥ax+b≥
| 3 |
| 2 |
| 2 |
| 3 |
函数y=f(x)在区间(0,+∞)内可导,导函数f′(x)是减函数,且f′(x)＞0,设x0∈(0,+∞),y=kx+m是曲线y=f(x)在点(x0,f(x0))处的切线方程,并设函数g(x)=kx+m.
(1)用x0、f(x0)、f′(x0)表示m;
(2)证明当x0∈(0,+∞)时,g(x)≥f(x);
(3)若关于x的不等式x2+1≥ax+b≥
在
上恒成立,其中a、b为实数，求b的取值范围及a与b 所满足的关系.
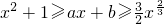在（0，+∞）上恒成立，其中a，b为实数，求b的取值范围及a，b所满足的关系．
在
上恒成立，其中a、b为实数，求b的取值范围及a与b所满足的关系。