摘要:(II)若数列满足证明是等差数列.
网址:http://m.1010jiajiao.com/timu_id_21120[举报]
称满足以下两个条件的有穷数列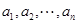 为
为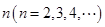 阶“期待数列”:
阶“期待数列”:
①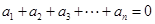 ;②
;②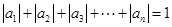 .
.
(1)若等比数列 为
为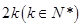 阶“期待数列”,求公比q及
阶“期待数列”,求公比q及 的通项公式;
的通项公式;
(2)若一个等差数列 既是
既是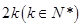 阶“期待数列”又是递增数列,求该数列的通项公式;
阶“期待数列”又是递增数列,求该数列的通项公式;
(3)记n阶“期待数列” 的前k项和为
的前k项和为 :
:
(i)求证: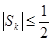 ;
;
(ii)若存在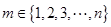 使
使 ,试问数列
,试问数列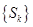 能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
查看习题详情和答案>>
称满足以下两个条件的有穷数列 为
为 阶“期待数列”:
阶“期待数列”:
① ;②
;② .
.
(1)若等比数列 为
为 阶“期待数列”,求公比q及
阶“期待数列”,求公比q及 的通项公式;
的通项公式;
(2)若一个等差数列 既是
既是 阶“期待数列”又是递增数列,求该数列的通项公式;
阶“期待数列”又是递增数列,求该数列的通项公式;
(3)记n阶“期待数列”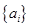 的前k项和为
的前k项和为 :
:
(i)求证: ;
;
(ii)若存在 使
使 ,试问数列
,试问数列 能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
能否为n阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.