网址:http://m.1010jiajiao.com/timu_id_21044[举报]
1-12题 AAAAA CDDCD BB
13、等腰梯形;14、 ;15、充分非必要;16、186
;15、充分非必要;16、186
17、
18、解:由 +25+|
+25+| -5
-5 |≥
|≥ ,而
,而 ,等号当且仅当
,等号当且仅当 时成立;且
时成立;且 ,等号当且仅当
,等号当且仅当 时成立;所以,
时成立;所以, ,等号当且仅当
,等号当且仅当 时成立;故
时成立;故 。
。
19、(Ⅰ) 表示当甲公司不投入宣传费时,乙公司要回避失败的风险至少要投入11万元的宣传费;
表示当甲公司不投入宣传费时,乙公司要回避失败的风险至少要投入11万元的宣传费; 表示当乙公司不投入宣传费时,甲公司要回避失败的风险至少要投入21万元的宣传费.
表示当乙公司不投入宣传费时,甲公司要回避失败的风险至少要投入21万元的宣传费.
(Ⅱ)设甲、乙公司投入的宣传费分别为 、
、 万元,当且仅当
万元,当且仅当 ①,
①,
且 ……②时双方均无失败的风险,
……②时双方均无失败的风险,
由①②得 易解得
易解得 ,
,
所以 ,故
,故 .
.
20、解:(1) 令g(x)=f(x)-2x=ln(x+m)-2x, 则g (x)=
(x)= -2
-2
∵x≥2-m ∴x+m≥2 ∴ ≤
≤ 从而g
从而g (x)=
(x)= -2≤
-2≤ -2<0
-2<0
∴g(x)在[2-m, +
 上单调递减 ∴x=2-m时,
上单调递减 ∴x=2-m时,
g(x)=f(x)-2x最大值=ln(2-m+m)-2(2-m)=ln2+
(2) 假设f(x)=x还有另一解x= (
(

 ) 由假设知
) 由假设知
 -
- =f(
=f( )-f(
)-f( )=f
)=f (x
(x )?(
)?( -
- ) x
) x
 [2-m, +
[2-m, +

故f (x
(x )=1, 又∵f
)=1, 又∵f (x
(x )=
)= ≤
≤ <1 矛盾
<1 矛盾
故f(x)=x有唯一解x=
21、
22、解:(1)若
 ,则在定义域内存在
,则在定义域内存在 ,
,
使得 ,∵方程
,∵方程 无解,
无解,
∴
 .
.
 ,
,
当 时,
时, , 当
, 当 时,由
时,由 ,
,
得 。
。
∴ .
.
 ,
,
又∵函数 图象与函数
图象与函数 的图象有交点,设交点的横坐标为
的图象有交点,设交点的横坐标为 ,
,
则 ,其中
,其中 ,
,
∴ ,即
,即 .
.
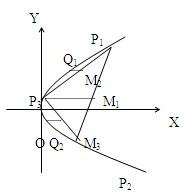 已知抛物线y2=2x.
已知抛物线y2=2x.(1)在抛物线上任取二点P1(x1,y1),P2(x2,y2),经过线段P1P2的中点作直线平行于抛物线的轴,和抛物线交于点P3,证明△P1P2P3的面积为
| 1 | 16 |
(2)经过线段P1P3、P2P3的中点分别作直线平行于抛物线的轴,与抛物线依次交于Q1、Q2,试将△P1P3Q1与△P2P3Q2的面积和用y1,y2表示出来;
(3)仿照(2)又可做出四个更小的三角形,如此继续下去可以做一系列的三角形,由此设法求出线段P1P2与抛物线所围成的图形的面积. 查看习题详情和答案>>
(1)在抛物线上任取二点P1(x1,y1),P2(x2,y2),经过线段P1P2的中点作直线平行于抛物线的轴,和抛物线交于点P3,证明△P1P2P3的面积为
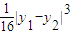 ;
;(2)经过线段P1P3、P2P3的中点分别作直线平行于抛物线的轴,与抛物线依次交于Q1、Q2,试将△P1P3Q1与△P2P3Q2的面积和用y1,y2表示出来;
(3)仿照(2)又可做出四个更小的三角形,如此继续下去可以做一系列的三角形,由此设法求出线段P1P2与抛物线所围成的图形的面积.
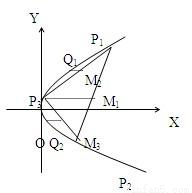 查看习题详情和答案>>
查看习题详情和答案>>
 ,且与椭圆
,且与椭圆 有共同的焦点.
有共同的焦点.(1)求此双曲线的标准方程;
(2)(普通中学学生做)设直线L:y=kx+3与双曲线交于A、B两点,试问:是否存在实数k,使得以弦AB为直径的圆过点O?若存在,求出k的值,若不存在,请说明理由.
(重点中学学生做)设直线L:y=kx+3与双曲线交于A、B两点,C是直线L1:y=mx+6上任一点(A、B、C三点不共线)试问:是否存在实数k,使得△ABC是以AB为底边的等腰三角形?若存在,求出k的值,若不存在,请说明理由.
查看习题详情和答案>>