摘要：S(0.0.2).M(1..0).N(0..).
网址：http://m.1010jiajiao.com/timu_id_20346[举报]
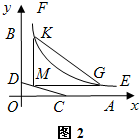
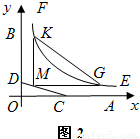
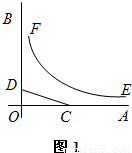
如图1，OA，OB是某地一个湖泊的两条互相垂直的湖堤，线段CD和曲线段EF分别是湖泊中的一座栈桥和一条防波堤．为观光旅游的需要，拟过栈桥CD上某点M分别修建与OA，OB平行的栈桥MG、MK，且以MG、MK为边建一个跨越水面的三角形观光平台MGK．建立如图2所示的直角坐标系，测得线段CD的方程是x+2y=20（0≤x≤20），曲线段EF的方程是xy=200（5≤x≤40），设点M的坐标为（s，t），记z=s•t．（题中所涉及的长度单位均为米，栈桥和防波堤都不计宽度（1）求z的取值范围；
（2）试写出三角形观光平台MGK面积S△MGK关于z的函数解析式，并求出该面积的最小值． 查看习题详情和答案>>
已知B1（0，1），B2（0，-1），M（1，0），动点P（x，y）满足直线PB1，PB2的斜率之积为-
．
（1）求点P的轨迹C的方程；
（2）设轨迹C与x轴的左，右两个交点分别为A1，A2，过点M作直线l和轨迹C分别交于点D1，D2．
（ⅰ）求证：直线A1D1，A1D2的斜率之积为定值；
（ⅱ）设直线A1D1，A2D2的交点为S，求证：点S在定直线上，并求出该定直线的方程．
查看习题详情和答案>>
| 1 | 4 |
（1）求点P的轨迹C的方程；
（2）设轨迹C与x轴的左，右两个交点分别为A1，A2，过点M作直线l和轨迹C分别交于点D1，D2．
（ⅰ）求证：直线A1D1，A1D2的斜率之积为定值；
（ⅱ）设直线A1D1，A2D2的交点为S，求证：点S在定直线上，并求出该定直线的方程．
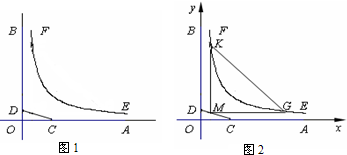
如图1，OA，OB是某地一个湖泊的两条垂直的湖堤，线段CD和曲线EF分别是湖泊中的一条栈桥和防波堤．为观光旅游需要，拟过栈桥CD上某点M分别修建与OA，OB平行的栈桥MG，MK，且以MG，MK为边建一个跨越水面的三角形观光平台MGK．建立如图2所示的直角坐标系，测得CD的方程是x+2y=20（0≤x≤20），曲线EF的方程是xy=200（x＞0），设点M的坐标为（s，t）．（题中所涉及长度单位均为米，栈桥及防波堤都不计宽度）
（1）求三角形观光平台MGK面积的最小值；
（2）若要使△MGK的面积不小于320平方米，求t的取值范围．
查看习题详情和答案>>
（1）求三角形观光平台MGK面积的最小值；
（2）若要使△MGK的面积不小于320平方米，求t的取值范围．
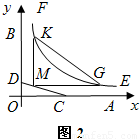
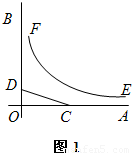
如图1，OA，OB是某地一个湖泊的两条互相垂直的湖堤，线段CD和曲线段EF分别是湖泊中的一座栈桥和一条防波堤．为观光旅游的需要，拟过栈桥CD上某点M分别修建与OA，OB平行的栈桥MG、MK，且以MG、MK为边建一个跨越水面的三角形观光平台MGK．建立如图2所示的直角坐标系，测得线段CD的方程是x+2y=20（0≤x≤20），曲线段EF的方程是xy=200（5≤x≤40），设点M的坐标为（s，t），记z=s•t．（题中所涉及的长度单位均为米，栈桥和防波堤都不计宽度
（1）求z的取值范围；
（2）试写出三角形观光平台MGK面积S△MGK关于z的函数解析式，并求出该面积的最小值．
查看习题详情和答案>>
（1）求z的取值范围；
（2）试写出三角形观光平台MGK面积S△MGK关于z的函数解析式，并求出该面积的最小值．
查看习题详情和答案>>
如图1，OA，OB是某地一个湖泊的两条互相垂直的湖堤，线段CD和曲线段EF分别是湖泊中的一座栈桥和一条防波堤．为观光旅游的需要，拟过栈桥CD上某点M分别修建与OA，OB平行的栈桥MG、MK，且以MG、MK为边建一个跨越水面的三角形观光平台MGK．建立如图2所示的直角坐标系，测得线段CD的方程是x+2y=20（0≤x≤20），曲线段EF的方程是xy=200（5≤x≤40），设点M的坐标为（s，t），记z=s•t．（题中所涉及的长度单位均为米，栈桥和防波堤都不计宽度
（1）求z的取值范围；
（2）试写出三角形观光平台MGK面积S△MGK关于z的函数解析式，并求出该面积的最小值．
查看习题详情和答案>>
（1）求z的取值范围；
（2）试写出三角形观光平台MGK面积S△MGK关于z的函数解析式，并求出该面积的最小值．
查看习题详情和答案>>