摘要：由(Ⅰ)知当时,

网址：http://m.1010jiajiao.com/timu_id_198553[举报]

（）（本小题满分12分）已知椭圆C: 的离心率为，过右焦点F的直线l与C相交于A、B两点，当l的斜率为1是，坐标原点O到直线l的距离为.

（Ⅰ）求a,b的值；

（Ⅱ）C上是否存在点P，使得当l绕F转到某一位置时，有成立？

若存在，求出所有的P的坐标与l的方程；若不存在，说明理由.

 查看习题详情和答案>>
（1）已知α，β∈(0，
π
2
)，且tanα•tanβ＜1，比较α+β与
π
2
的大小；
（2）试确定一个区间D，D⊆(-
π
2
，
π
2
)，对任意的α、β∈D，当α+β＜
π
2
时，恒有sinα＜cosβ；并说明理由．
说明：对于第（2）题，将根据写出区间D所体现的思维层次和对问题探究的完整性，给予不同的评分． 查看习题详情和答案>>
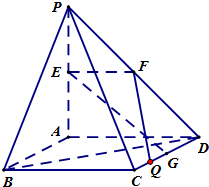精英家教网（理）如图，PA⊥平面ABCD，四边形ABCD是正方形，PA=AD=2，点E、F、G分别为线段PA、PD和CD的中点．
（1）求异面直线EG与BD所成角的大小；
（2）在线段CD上是否存在一点Q，使得点A到平面EFQ的距离恰为
4
5
？若存在，求出线段CQ的长；若不存在，请说明理由．
（文）已知坐标平面内的一组基向量为
e
1=(1，sinx)，
e
2=(0，cosx)，其中x∈[0，
π
2
)，且向量
a
=
1
2
e
1+
3
2
e
2．
（1）当
e
1和
e
2都为单位向量时，求|
a
|；
（2）若向量
a
和向量
b
=(1，2)共线，求向量
e
1和
e
2的夹角． 查看习题详情和答案>>
由函数y=f（x）确定数列{an}，an=f（n），函数y=f（x）的反函数y=f-1（x）能确定数列bn，bn=f-1（n）若对于任意n∈N*都有bn=an，则称数列{bn}是数列{an}的“自反函数列”
（1）设函数f（x）=
px+1
x+1
，若由函数f（x）确定的数列{an}的自反数列为{bn}，求an；
（2）已知正整数列{cn}的前项和sn=
1
2
（cn+
n
cn
）．写出Sn表达式，并证明你的结论；
（3）在（1）和（2）的条件下，d1=2，当n≥2时，设dn=
-1
anSn2
，Dn是数列{dn}的前n项和，且Dn＞loga（1-2a）恒成立，求a的取值范围． 查看习题详情和答案>>
由正态分布N（1，8）对应的曲线可知，当x=
 
时，函数P（x）有最大值，为
 
． 查看习题详情和答案>>

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网