摘要：(2)解:设方程ax2+bx+c＝0的两根为x1和x2,则x1+x2＝-,x1x2＝.|A1B1|2＝(x1-x2)2＝(x1+x2)2-4x1x2
网址：http://m.1010jiajiao.com/timu_id_198323[举报]
二次函数f(x)＝ax2＋bx＋c(a、b、c∈R，a≠0)．
(Ⅰ)对于x1、x2∈R，且x1＜x2，f(x1)≠f(x2)，求证：方程f(x)＝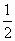
[f(x1)＋f(x2)]有不相等的两实根，且必有一根属于(x1、x2)；
(Ⅱ)若方程f(x)＝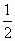
[f(x1)＋f(x2)]在(x1、x2)内的实根为m，且x1、m－
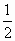、x2成等差数列，设x＝x0是f(x)的对称轴方程．
求证：x0＜m2；
(Ⅲ)若a＞0，f(0)＝1，方程f(x)＝x的两实根为α、β，当|β|＜2，
|α－β|＝2时，求b的取值范围．
查看习题详情和答案>>二次函数f(x)＝ax2＋bx＋c(a、b、c∈R，a≠0)．
(Ⅰ)对于x1、x2∈R，且x1＜x2，f(x1)≠f(x2)，求证：方程f(x)＝
[f(x1)＋f(x2)]有不相等的两实根，且必有一根属于(x1、x2)；
(Ⅱ)若方程f(x)＝
[f(x1)＋f(x2)]在(x1、x2)内的实根为m，且x1、m－
、x2成等差数列，设x＝x0是f(x)的对称轴方程．求证：x0＜m2．
(Ⅲ)若a＞0，f(0)＝1，方程f(x)＝x的两实根为α、β，当|β|＜2，|α－β|＝2时，求b的取值范围．
查看习题详情和答案>>已知函数y＝|x|＋1，y＝
，y＝
(x＋
)(x＞0)的最小值恰好是方程x3＋ax2＋bx＋c＝0的三个根，其中0＜t＜1．
(1)求证：a2＝2b＋3；
(2)设x1，x2是函数f(x)＝x3＋ax2＋bx＋c的两个极值点．若|x1－x2|＝
，求函数f(x)的解析式．
，y＝
(x＋
)，(x＞0)的最小值恰好是方程：x3＋ax2＋bx＋c＝0的三个根，其中0＜t＜1．
，求函数f(x)的解析式；
，y＝
(x＋
)(x＞0)的最小值恰好是方程x3＋ax2＋bx＋c＝0的三个根，其中0＜t＜1．
，求函数f(x)的解析式．