网址：http://m.1010jiajiao.com/timu_id_198204[举报]
定义：若存在常数k，使得对定义域D内的任意两个不同的实数x1，x2，均有
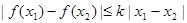成立，则称函数
在定义域D上满足利普希茨条件。对于函数
满足利普希茨条件，则常数k的最小值应是 （ ）
A．2 B．1 C．
D．
查看习题详情和答案>>
定义：若存在常数k，使得对定义域D内的任意两个不同的实数x1，x2，均有
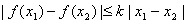成立，则称函数
在定义域D上满足利普希茨条件。对于函数
满足利普希茨条件，则常数k的最小值应是 （ ）
A．2 B．1 C．
D．
查看习题详情和答案>>
对于非空实数集A，记A*＝{y|?x∈A，y≥x}．设非空实数集合M、P满足：M⊆P，且若x＞1，则x∉P.现给出以下命题：
①对于任意给定符合题设条件的集合M、P，必有P*⊆M*；
②对于任意给定符合题设条件的集合M、P，必有M*∩P≠∅；
③对于任意给定符合题设条件的集合M、P，必有M∩P*＝∅；
④对于任意给定符合题设条件的集合M、P，必存在常数a，使得对任意的b∈M*，恒有a＋b∈P*.其中正确的命题是( )
A．①③ B．③④
C．①④ D．②③
查看习题详情和答案>>
（
，D是此函数的定义域），若同时满足下列条件：①
在D内单调递减或单调递增；②存在区间[a，b]
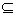D，使
在[a，b]上的值域为[a，b]；那么把
叫闭函数； （1）求闭函数
符合条件②的区间[a，b]；（2）判断函数
是否为闭函数？并说明理由；（3）
是闭函数，求实数k的取值范围。 ①方程f(x)-x=0有实数根；②函数f(x)的导函数f′(x)满足0＜f′(x)＜1.
(1)判断函数f(x)=
x+
sinx是否是集合M中的元素，并说明理由；
(2)集合M中的元素f(x)具有下列性质：
若f(x)的定义域为I,则对于任意［m,n］
I都存在x0∈［m,n］，使得等式f(n)-f(m)=(n-m)f′(x0)成立.
请利用这一性质证明：方程f(x)-x=0有唯一的实数根；
(3)若存在实数x1,使得M中元素f(x)定义域中的任意实数a、b都有|a-x1|＜1和|b-x1|＜1成立，证明：|f(b)-f(a)|＜2.
查看习题详情和答案>>