摘要：.所以.同理.
网址：http://m.1010jiajiao.com/timu_id_198087[举报]
（理）定义：若存在常数k，使得对定义域D内的任意两个不同的实数x1，x2，均有：|f（x1）-f（x2）|≤k|x1-x2|成立，则称f（x）在D上满足利普希茨（Lipschitz）条件．
（1）试举出一个满足利普希茨（Lipschitz）条件的函数及常数k的值，并加以验证；
（2）若函数f(x)=
在[1，+∞)上满足利普希茨（Lipschitz）条件，求常数k的最小值；
（3）现有函数f（x）=sinx，请找出所有的一次函数g（x），使得下列条件同时成立：
①函数g（x）满足利普希茨（Lipschitz）条件；
②方程g（x）=0的根t也是方程f(
)=
sin(
-
)=-
cos
=-1；
③方程f（g（x））=g（f（x））在区间[0，2π）上有且仅有一解．
查看习题详情和答案>>
（1）试举出一个满足利普希茨（Lipschitz）条件的函数及常数k的值，并加以验证；
（2）若函数f(x)=
| x+1 |
（3）现有函数f（x）=sinx，请找出所有的一次函数g（x），使得下列条件同时成立：
①函数g（x）满足利普希茨（Lipschitz）条件；
②方程g（x）=0的根t也是方程f(
| 3π |
| 4 |
| 2 |
| 3π |
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
③方程f（g（x））=g（f（x））在区间[0，2π）上有且仅有一解．
心理学研究表明，学生在课堂上各时段的接受能力不同。上课开始时，学生的兴趣高昂，接受能力渐强，随后有一段不太长的时间，学生的接受能力保持较理想的状态；渐渐地学生的注意力开始分散，接受能力渐弱并趋于稳定．设上课开始
分钟时，学生的接受能力为
（值越大，表示接受能力越强），与的函数关系为：
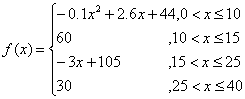
（1）开讲后多少分钟，学生的接受能力最强？能维持多少时间？
（2）试比较开讲后5分钟、20分钟、35分钟，学生的接受能力的大小；
（3）若一个数学难题，需要56的接受能力(即
)以及12分钟时间，老师能否及时在学生一直达到所需接受能力的状态下讲述完这个难题？
），则P在原直角坐标系中的坐标为________．
