摘要：推导过程为:祖?原理→柱体体积棱锥台体应用过程为:公式法.割补法.等积法[教学难点]割补法[教学重点]公式的推导及总结[教学流程]一.公式推导:通过一摞书演示.说明祖?原理:两个登高的几何体.若在所有高处的截面面积相等.则此两个几何体的体积相等
网址：http://m.1010jiajiao.com/timu_id_196281[举报]
一种十字绣作品由相同的小正方形构成，图①，②，③，④分别是制作该作品前四步时对应的图案，按照如此规律，第n步完成时对应图案中所包含小正方形的个数记为f（n）．
（1）求出f（2），f（3），f（4），f（5）的值；
（2）利用归纳推理，归纳出f（n+1）与f（n）的关系式；
（3）猜想f（n）的表达式，并写出推导过程．
查看习题详情和答案>>
（1）求出f（2），f（3），f（4），f（5）的值；
（2）利用归纳推理，归纳出f（n+1）与f（n）的关系式；
（3）猜想f（n）的表达式，并写出推导过程．
（理科）给出下面四个推导过程：其中正确的推导为
①∵a，b∈R+，∴
+
≥2
=2；
②∵x，y∈R+，∴lgx+lgy≥2
；
③∵a∈R，a≠0，∴
+a≥2
=4；
④∵x，y∈R，xy＜0，∴
+
=-[（-
）+（-
）]≤-2
=-2．
查看习题详情和答案>>
①④
①④
①∵a，b∈R+，∴
| b |
| a |
| a |
| b |
|
②∵x，y∈R+，∴lgx+lgy≥2
| lgx•lgy |
③∵a∈R，a≠0，∴
| 4 |
| a |
|
④∵x，y∈R，xy＜0，∴
| x |
| y |
| y |
| x |
| x |
| y |
| y |
| x |
(-
|
已知函数f（x）=x3-3x+1（x∈R）
（1）试利用单调性定义推导函数f（x）在给定区间[1，3]上的单调性；
（2）分析（1）的推导过程，说出函数f（x）的一个单调递增区间为
（3）分析（1）的推导过程，说出函数f（x）的一个单调递减区间为
（第（1）小题参考公式：a3-b3=（a-b）（a2+ab+b2））
查看习题详情和答案>>
（1）试利用单调性定义推导函数f（x）在给定区间[1，3]上的单调性；
（2）分析（1）的推导过程，说出函数f（x）的一个单调递增区间为
[1，+∞）
[1，+∞）
（不必证明）；（3）分析（1）的推导过程，说出函数f（x）的一个单调递减区间为
（-∞，1]
（-∞，1]
（不必证明）．（第（1）小题参考公式：a3-b3=（a-b）（a2+ab+b2））
和直线
，
所围成的平面图形，绕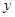
轴旋转一周所得到的旋转体为
；由同时满足
，
，
，
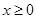的点
构成的平面图形,绕
.根据祖暅原理等知识，通过考察
和直线
，
所围成的平面图形，绕
轴旋转一周所得到的旋转体为
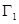；由同时满足
，
，
，
的点
构成的平面图形,绕
.根据祖暅原理等知识，通过考察
B．
C．
D．