摘要:解:(1)对数函数y=logax在上a>1时是增函数.0<a<1时是减函数,于是a>1时.loga5.1<loga5.9; 0<a<1时.loga5.1>loga5.9(2)[方法一] log 67 >log66=1=log77>log 7 6
网址:http://m.1010jiajiao.com/timu_id_194538[举报]
设f(x)=
且a≠1),函数y=g(x)的图象与函数y=f(x)图象关于直线x-y=0对称.
(1)求函数y=g(x)的解析式及定义域;
(2)设关于x的方程loga
=g(x)在[2,6]上有实数解,求t的取值范围;
(3)当a=e(e为自然对数的底数)时,证明:
g(k)>
.
查看习题详情和答案>>
| 1+ax |
| 1-ax |
(1)求函数y=g(x)的解析式及定义域;
(2)设关于x的方程loga
| t |
| (x2-1)(7-x) |
(3)当a=e(e为自然对数的底数)时,证明:
| n |
 |
| k=2 |
| 2-n-n2 | ||
|
设f(x)=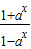 且a≠1),函数y=g(x)的图象与函数y=f(x)图象关于直线x-y=0对称.
且a≠1),函数y=g(x)的图象与函数y=f(x)图象关于直线x-y=0对称.
(1)求函数y=g(x)的解析式及定义域;
(2)设关于x的方程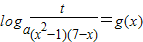 在[2,6]上有实数解,求t的取值范围;
在[2,6]上有实数解,求t的取值范围;
(3)当a=e(e为自然对数的底数)时,证明: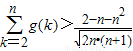 .
.
查看习题详情和答案>>
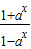 且a≠1),函数y=g(x)的图象与函数y=f(x)图象关于直线x-y=0对称.
且a≠1),函数y=g(x)的图象与函数y=f(x)图象关于直线x-y=0对称.(1)求函数y=g(x)的解析式及定义域;
(2)设关于x的方程
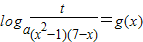 在[2,6]上有实数解,求t的取值范围;
在[2,6]上有实数解,求t的取值范围;(3)当a=e(e为自然对数的底数)时,证明:
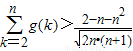 .
.查看习题详情和答案>>
给出下列命题:
①命题“若x≠1且y≠2,则(x-1)2+(y-2)2≠0”为真命题;
②函数f(x)=lnx+x-
在区间(1,2)上有且仅有一个零点;
③不等式
(x-2)≥0的解集为[2,+∞];
④函数y=x+
(x≥3)的最小值为3
其中正确的序号是
查看习题详情和答案>>
①命题“若x≠1且y≠2,则(x-1)2+(y-2)2≠0”为真命题;
②函数f(x)=lnx+x-
| 3 |
| 2 |
③不等式
| x-1 |
④函数y=x+
| 1 |
| x-1 |
其中正确的序号是
①②
①②
(把你认为正确命题的序号都填上)