题目内容
给出下列命题:
①命题“若x≠1且y≠2,则(x-1)2+(y-2)2≠0”为真命题;
②函数f(x)=lnx+x-
在区间(1,2)上有且仅有一个零点;
③不等式
(x-2)≥0的解集为[2,+∞];
④函数y=x+
(x≥3)的最小值为3
其中正确的序号是
①命题“若x≠1且y≠2,则(x-1)2+(y-2)2≠0”为真命题;
②函数f(x)=lnx+x-
| 3 |
| 2 |
③不等式
| x-1 |
④函数y=x+
| 1 |
| x-1 |
其中正确的序号是
①②
①②
(把你认为正确命题的序号都填上)分析:设P(x,y)为平面直角坐标系内点,当x≠1,且y≠2时,P点不取(1,2),则P点到(1,2)距离的平方就不可能为零;f(1)•f(2)<0,f(x)在(1,2)上连续且单调递增,故有且只有一个零点;由于
≥,故不等式可化为
=0或
或
,解得x∈{1}∪[2,+∞);由x≥3,知x-1>0,故y=(x-1)+
+1≥2
=3,故此函数无法取到最小值3.
| x-1 |
| x-1 |
|
|
| 1 |
| x-1 |
(x-1)×
|
解答:解:①设P(x,y)为平面直角坐标系内点,
当x≠1,且y≠2时,P点不取(1,2),则P点到(1,2)距离的平方就不可能为零,故①为真命题;
②f(1)•f(2)<0,f(x)在(1,2)上连续且单调递增,
故有且只有一个零点,故②为真命题;
③由于
≥0,故不等式可化为
=0或
或
,
解得x∈{1}∪[2,+∞),故③不正确;
∵x≥3,∴x-1>0,
则y=(x-1)+
+1≥2
=3,
当且仅当x=2时,等号成立,故此函数无法取到最小值3,故④不正确.
故答案为:①②.
当x≠1,且y≠2时,P点不取(1,2),则P点到(1,2)距离的平方就不可能为零,故①为真命题;
②f(1)•f(2)<0,f(x)在(1,2)上连续且单调递增,
故有且只有一个零点,故②为真命题;
③由于
| x-1 |
| x-1 |
|
|
解得x∈{1}∪[2,+∞),故③不正确;
∵x≥3,∴x-1>0,
则y=(x-1)+
| 1 |
| x-1 |
(x-1)×
|
当且仅当x=2时,等号成立,故此函数无法取到最小值3,故④不正确.
故答案为:①②.
点评:本题考查命题的真假判断,是基础题.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
相关题目
 y =
y = 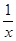 的一个交点;
的一个交点; 的一个交点
的一个交点 的一个交点
的一个交点 (
( 的一个交点;
的一个交点; 的一个交点;
的一个交点; 的一个交点;
的一个交点; (
(