摘要：[方法一] a== ① b== ②.
网址：http://m.1010jiajiao.com/timu_id_194502[举报]
设A是由m×n个实数组成的m行n列的数表，满足：每个数的绝对值不大于1，且所有数的和为零，记s(m，n)为所有这样的数表构成的集合。
对于A∈S(m,n),记ri(A)为A的第ⅰ行各数之和（1≤ⅰ≤m），Cj(A)为A的第j列各数之和（1≤j≤n）：
记K(A)为∣r1(A)∣,∣R2(A)∣,…,∣Rm(A)∣,∣C1(A)∣,∣C2(A)∣,…,∣Cn(A)∣中的最小值。
（1） 对如下数表A，求K（A）的值；
|
1 |
1 |
-0.8 |
|
0.1 |
-0.3 |
-1 |
（2）设数表A∈S（2,3）形如
|
1 |
1 |
c |
|
a |
b |
-1 |
求K（A）的最大值；
（3）给定正整数t，对于所有的A∈S（2,2t+1），求K（A）的最大值。
【解析】（1）因为
，
所以
（2） 不妨设
.由题意得
.又因为
，所以
，
于是
，
，
所以
，当
，且
时，
取得最大值1。
（3）对于给定的正整数t，任给数表
如下，
|
|
|
… |
|
|
|
|
… |
|
任意改变A的行次序或列次序，或把A中的每一个数换成它的相反数，所得数表
，并且
，因此，不妨设
，
且
。
由
得定义知，
，
又因为
所以
所以，
对数表
：
|
1 |
1 |
… |
1 |
|
… |
|
|
|
|
… |
|
-1 |
… |
-1 |
则
且
，
综上，对于所有的，的最大值为
查看习题详情和答案>>
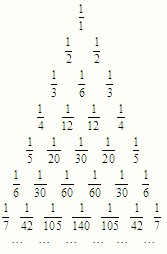将杨晖三角形中的每一个数Cnr都换成分数 | 1 | ||
(n+1)
|
| 1 |
| 3 |
| 1 |
| 12 |
| 1 |
| 30 |
| 1 |
| 60 |
| 1 | ||
n
|
| 1 | ||
(n+1)
|
观察莱布尼兹三角形规律，计算极限
| lim |
| n→∞ |
| 1 |
| 2 |
| 1 |
| 2 |
（2010•武清区一模）将杨辉三角中的奇数换成1，偶数换成0，便可以得到如下的“0-1三角”．在“0-1三角”中，从第1行起，设第n（n∈N*）次出现全行为1时，1的个数为an，则a3等于（ ）
查看习题详情和答案>>
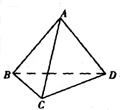数学课上，张老师用六根长度均为a的塑料棒搭成了一个正三棱锥（如图所示），然后他将其中的两根换成长度分别为在