摘要：[教学重点]1.根式的概念. 2.n次方根的性质.
网址：http://m.1010jiajiao.com/timu_id_194063[举报]
某市十所重点中学进行高二联考，共有5000名考生，为了了解数学学科的学习情况，现从中随机抽出若干名学生在这次测试中的数学成绩，制成如下频率分布表：
（1）根据上面频率分布表，推出①，②，③，④处的数值分别为 ， ， ；
（2）在所给的坐标系中画出区间[80，150]上的频率分布直方图；
（3）根据题中信息估计总体：（ⅰ）120分及以上的学生数；（ⅱ）平均分． 查看习题详情和答案>>
（1）根据上面频率分布表，推出①，②，③，④处的数值分别为
（2）在所给的坐标系中画出区间[80，150]上的频率分布直方图；
（3）根据题中信息估计总体：（ⅰ）120分及以上的学生数；（ⅱ）平均分． 查看习题详情和答案>>
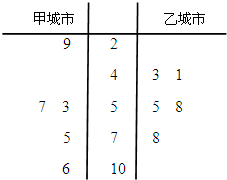（2013•朝阳区一模）国家环境标准制定的空气质量指数与空气质量等级对应关系如下表：| 空气质量指数 | 0-50 | 51-100 | 101-150 | 151-200 | 201-300 | 300以上 |
| 空气质量等级 | 1级优 | 2级良 | 3级轻度污染 | 4级中度污染 | 5级重度污染 | 6级严重污染 |
（Ⅰ）试根据上面的统计数据，判断甲、乙两个城市的空气质量指数的方差的大小关系（只需写出结果）；
（Ⅱ）试根据上面的统计数据，估计甲城市某一天空气质量等级为2级良的概率；
（Ⅲ）分别从甲城市和乙城市的统计数据中任取一个，试求这两个城市空气质量等级相同的概率．
（注：s2=
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
. |
| x |
已知抛物线y2=2px（p＞0），点P（
，
），线段OP的垂直平分线经过抛物线的焦点F，经过F作两条互相垂直的弦AB、CD、，设AB、CD的重点分别为M、N
（1）求抛物线的方程；
（2）直线MN是否经过定点？若经过，求出定点坐标；若不经过，试说明理由． 查看习题详情和答案>>
| 8 |
| 5 |
| 4 |
| 5 |
（1）求抛物线的方程；
（2）直线MN是否经过定点？若经过，求出定点坐标；若不经过，试说明理由． 查看习题详情和答案>>
一名高二学生盼望进入某名牌大学学习，不放弃能考入该大学的任何一次机会．已知该大学通过以下任何一种方式都可被录取：
①2010年2月国家数学奥赛集训队考试通过（集训队从2009年10月省数学竞赛壹等奖获得者中选拔，通过考试进入集训队则能被该大学提前录取）；
②2010年3月自主招生考试通过并且2010年6月高考分数达重点线；
③2010年6月高考达到该校录取分数线（该校录取分数线高于重点线）．
该名考生竞赛获省一等奖．自主招生考试通过．高考达重点线．高考达该校分数线等事件的概率如下表：
如果数学竞赛获省一等奖，该学生估计自己进入国家集训队的概率是0.4．
（1）求该学生参加自主招生考试的概率；
（2）求该学生参加考试次数的分布列与数学期望；
（3）求该学生被该大学录取的概率．
查看习题详情和答案>>
①2010年2月国家数学奥赛集训队考试通过（集训队从2009年10月省数学竞赛壹等奖获得者中选拔，通过考试进入集训队则能被该大学提前录取）；
②2010年3月自主招生考试通过并且2010年6月高考分数达重点线；
③2010年6月高考达到该校录取分数线（该校录取分数线高于重点线）．
该名考生竞赛获省一等奖．自主招生考试通过．高考达重点线．高考达该校分数线等事件的概率如下表：
| 事件 | 省数学竞获一等奖 | 自主招生考试通过 | 高考达重点线 | 高考达该校分数线 |
| 概率 | 0.5 | 0.7 | 0.8 | 0.6 |
（1）求该学生参加自主招生考试的概率；
（2）求该学生参加考试次数的分布列与数学期望；
（3）求该学生被该大学录取的概率．
