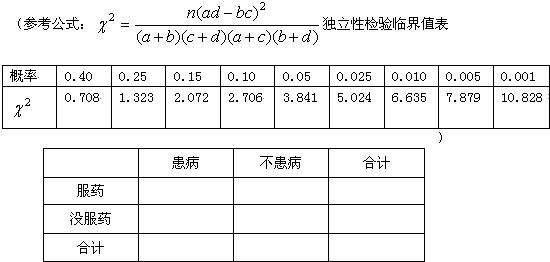
题目内容
为考察某种药物预防疾病的效果,进行动物试验,得到如下丢失数据的列联表:药物效果试验列联表
工作人员曾用分层抽样的方法从50只服用药的动物中抽查10个进行重点跟踪试验.知道其中患病的有2只.
(1)求出列联表中数据x,y,M,N的值;
(2)通过所给的数据判断药物是否有效;
(3)能够以97.5%的把握认为药物有效吗?
参考数据:

分析:(1)用分层抽样的方法,从50只服用药的动物中抽查10个进行重点跟踪试验,其中患病的有2只,这样可以列出比例式,求出x的值,根据列联表中各个数据的关系,得到另外三个值.
(2)从50只服用药的动物中抽查10个进行重点跟踪试验.知道其中患病的有2只,得到服药的又患病的概率,从中抽取两个人变量表示患病的人数,ξ取值为0,1,2,结合变量对应的事件得到分布列和患病的期望.同理做出不服药患病的期望,两个期望进行比较,得到药物有效的结论.
(3)根据列联表中的数据代入求观测值的公式,做出观测值,把所得的观测值同参考数据进行比较,发现4.76<5.204,得到没有97.5%的把握认为药物有效.
(2)从50只服用药的动物中抽查10个进行重点跟踪试验.知道其中患病的有2只,得到服药的又患病的概率,从中抽取两个人变量表示患病的人数,ξ取值为0,1,2,结合变量对应的事件得到分布列和患病的期望.同理做出不服药患病的期望,两个期望进行比较,得到药物有效的结论.
(3)根据列联表中的数据代入求观测值的公式,做出观测值,把所得的观测值同参考数据进行比较,发现4.76<5.204,得到没有97.5%的把握认为药物有效.
解答:解:(1)∵用分层抽样的方法,
从50只服用药的动物中抽查10个进行重点跟踪试验,其中患病的有2只,
∴
=
,
∴x=10,
∴y=50-10=40,
∴M=20+10=30,N=30+40=70,
即x=10,y=40,M=30,N=70.
(2)从50只服用药的动物中抽查10个进行重点跟踪试验.知道其中患病的有2只,
得到服药的又患病的概率,从中抽取两个人变量表示患病的人数,
ξ取值为0,1,2,
P(ξ=0)=
=
,P(ξ=1)=
=
,P(ξ=2)=
=
,

Eξ=
,
P(η=0)=
=
,P(η=1)=
=
P(η=2)=
=

•Eη=
•∴Eξ<Eη说明药物有效
(3)由表格可以得到
∵K2=
≈4.76<5.204
由参考数据知不能够以97.5%的把握认为药物有效.
从50只服用药的动物中抽查10个进行重点跟踪试验,其中患病的有2只,
∴
| 2 |
| 10 |
| x |
| 50 |
∴x=10,
∴y=50-10=40,
∴M=20+10=30,N=30+40=70,
即x=10,y=40,M=30,N=70.
(2)从50只服用药的动物中抽查10个进行重点跟踪试验.知道其中患病的有2只,
得到服药的又患病的概率,从中抽取两个人变量表示患病的人数,
ξ取值为0,1,2,
P(ξ=0)=
| ||
|
| 38 |
| 245 |
| ||||
|
| 120 |
| 245 |
| ||
|
| 87 |
| 245 |

Eξ=
| 294 |
| 245 |
P(η=0)=
| ||
|
| 9 |
| 245 |
| ||||
|
| 80 |
| 245 |
P(η=2)=
| ||
|
| 156 |
| 245 |

•Eη=
| 392 |
| 245 |
•∴Eξ<Eη说明药物有效
(3)由表格可以得到
∵K2=
| 100(800-300)2 |
| 30×70×50×50 |
由参考数据知不能够以97.5%的把握认为药物有效.
点评:本题考查独立性检验的列联表,考查独立性检验的观测值,考查判断服药对于患病是否有效,是一个综合题,这种问题只有个别的省份作为高考题出现过,要引起注意.

练习册系列答案
相关题目