摘要:(Ⅲ)若直线与函数的图象有3个交点.求的取值范围.
网址:http://m.1010jiajiao.com/timu_id_192894[举报]
命题
①函数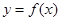 的图象与直线
的图象与直线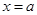 最多有一个交点;
最多有一个交点;
②函数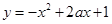 在区间
在区间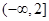 上单调递增,则
上单调递增,则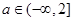 ;
;
③若 ,当
,当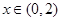 时,
时, ,则
,则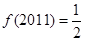 ;
;
④函数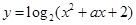 的值域为R,则实数
的值域为R,则实数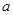 的取值范围是
的取值范围是 ;
;
⑤函数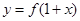 与
与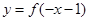 的图象关于
的图象关于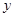 轴对称;
轴对称;
以上命题正确的个数有( )个
A、2 B、3 C、4 D、5
查看习题详情和答案>>
命题
①函数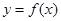 的图象与直线
的图象与直线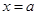 最多有一个交点;
最多有一个交点;
②函数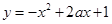 在区间
在区间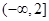 上单调递增,则
上单调递增,则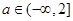 ;
;
③若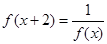 ,当
,当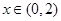 时,
时,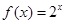 ,则
,则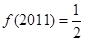 ;
;
④函数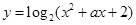 的值域为R,则实数
的值域为R,则实数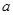 的取值范围是
的取值范围是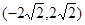 ;
;
⑤函数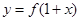 与
与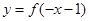 的图象关于
的图象关于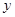 轴对称;
轴对称;
以上命题正确的个数有( )个
①函数
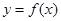 的图象与直线
的图象与直线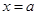 最多有一个交点;
最多有一个交点;②函数
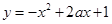 在区间
在区间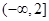 上单调递增,则
上单调递增,则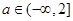 ;
;③若
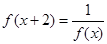 ,当
,当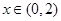 时,
时,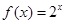 ,则
,则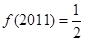 ;
;④函数
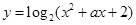 的值域为R,则实数
的值域为R,则实数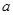 的取值范围是
的取值范围是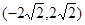 ;
;⑤函数
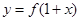 与
与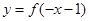 的图象关于
的图象关于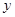 轴对称;
轴对称;以上命题正确的个数有( )个
| A.2 | B.3 | C.4 | D.5 |
命题
①函数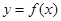 的图象与直线
的图象与直线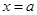 最多有一个交点;
最多有一个交点;
②函数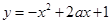 在区间
在区间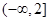 上单调递增,则
上单调递增,则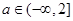 ;
;
③若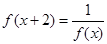 ,当
,当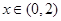 时,
时,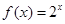 ,则
,则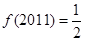 ;
;
④函数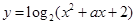 的值域为R,则实数
的值域为R,则实数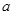 的取值范围是
的取值范围是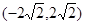 ;
;
⑤函数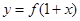 与
与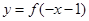 的图象关于
的图象关于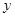 轴对称;
轴对称;
以上命题正确的个数有( )个
| A.2 | B.3 | C.4 | D.5 |
映射与函数:若A∈{1,2,3,4},B∈{a,b,c};问:A到B的映射有 个,B到A的映射有 个;A到B的函数有 个,若A∈{1,2,3},则A到B的一一映射有 个,函数y=φ(x)的图象与直线x=a交点的个数为 个.
查看习题详情和答案>>
已知函数 的一系列对应值如下表:
的一系列对应值如下表:
(1)根据表格提供的数据求函数y=f(x)的解析式;
(2)(文)当x∈[0,2π]时,求方程f(x)=2B的解.
(3)(理)若对任意的实数a,函数y=f(kx)(k>0), 的图象与直线y=1有且仅有两个不同的交点,又当
的图象与直线y=1有且仅有两个不同的交点,又当 时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
查看习题详情和答案>>
 的一系列对应值如下表:
的一系列对应值如下表:| x |  |  |  |  |  |  |  |
| y | -1 | 1 | 3 | 1 | -1 | 1 | 3 |
(2)(文)当x∈[0,2π]时,求方程f(x)=2B的解.
(3)(理)若对任意的实数a,函数y=f(kx)(k>0),
 的图象与直线y=1有且仅有两个不同的交点,又当
的图象与直线y=1有且仅有两个不同的交点,又当 时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.查看习题详情和答案>>