题目内容
已知函数 的一系列对应值如下表:
的一系列对应值如下表:| x |  |  |  |  |  |  |  |
| y | -1 | 1 | 3 | 1 | -1 | 1 | 3 |
(2)(文)当x∈[0,2π]时,求方程f(x)=2B的解.
(3)(理)若对任意的实数a,函数y=f(kx)(k>0),
 的图象与直线y=1有且仅有两个不同的交点,又当
的图象与直线y=1有且仅有两个不同的交点,又当 时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
时,方程f(kx)=m恰有两个不同的解,求实数m的取值范围.
【答案】分析:(1)由已知中表格中提供的数据,我们可以判断出函数的最值及周期,进而A,B与最值的关系,ω与周期的关系,确定出A,B,ω的值,代入最大值点的坐标后,即可求出φ的值,进而得到函数的解析式.
(2)由(1)中所得的B值,我们可以构造出一个三角方程,根据正弦函数的性质及已知中x∈[0,2π],可求出对应的x值,得到答案.
(3)若函数y=f(kx)(k>0), 的图象与直线y=1有且仅有两个不同的交点,则函数的周期为
的图象与直线y=1有且仅有两个不同的交点,则函数的周期为 ,又由当
,又由当 时,方程f(kx)=m恰有两个不同的解,我们可以构造出一个关于m的不等式,解不等式即可得到实数m的取值范围.
时,方程f(kx)=m恰有两个不同的解,我们可以构造出一个关于m的不等式,解不等式即可得到实数m的取值范围.
解答: 解:(1)依题意,
解:(1)依题意, ,∴ω=1(2分)
,∴ω=1(2分)
又 ,解得
,解得 (5分)
(5分)
 ,解得
,解得 (7分)
(7分)
∴ 为所求.(8分)
为所求.(8分)
(2)文:由f(x)=2B,得 (10分)
(10分)
∵x∈[0,2π],∴ (12分)
(12分)
∴ 或
或 ,即
,即 为所求.(14分)
为所求.(14分)
(3)理:由已知条件可知,函数 的周期为
的周期为 ,
,
又k>0,∴k=3(10分)
令 ,∵
,∵ ,
,
∴
而sint在 上单调递增,在
上单调递增,在 上单调递减,且
上单调递减,且 ,
,
如图∴sint=s在 上有两个不同的解的充要条件是
上有两个不同的解的充要条件是 ,(12分)
,(12分)
∴方程f(x)=m恰有两个不同的解的充要条件是 .(14分)
.(14分)
(注:单调区间写成 、
、 也行;直接数形结合得到正确结果,也可)
也行;直接数形结合得到正确结果,也可)
点评:本题考查的知识点是正弦型函数解析式的求法,三角方程的解法,正弦函数的图象和性质,其中(1)的关键是熟练掌握正弦型函数解析式中参数与函数性质的关系,(2)的关键是熟练掌握正弦型函数的性质,(3)的关键是将已知,结合正弦函数的性质,转化为一个关于m的不等式.
(2)由(1)中所得的B值,我们可以构造出一个三角方程,根据正弦函数的性质及已知中x∈[0,2π],可求出对应的x值,得到答案.
(3)若函数y=f(kx)(k>0),
 的图象与直线y=1有且仅有两个不同的交点,则函数的周期为
的图象与直线y=1有且仅有两个不同的交点,则函数的周期为 ,又由当
,又由当 时,方程f(kx)=m恰有两个不同的解,我们可以构造出一个关于m的不等式,解不等式即可得到实数m的取值范围.
时,方程f(kx)=m恰有两个不同的解,我们可以构造出一个关于m的不等式,解不等式即可得到实数m的取值范围.解答:
 解:(1)依题意,
解:(1)依题意, ,∴ω=1(2分)
,∴ω=1(2分)又
 ,解得
,解得 (5分)
(5分) ,解得
,解得 (7分)
(7分)∴
 为所求.(8分)
为所求.(8分)(2)文:由f(x)=2B,得
 (10分)
(10分)∵x∈[0,2π],∴
 (12分)
(12分)∴
 或
或 ,即
,即 为所求.(14分)
为所求.(14分)(3)理:由已知条件可知,函数
 的周期为
的周期为 ,
,又k>0,∴k=3(10分)
令
 ,∵
,∵ ,
,∴

而sint在
 上单调递增,在
上单调递增,在 上单调递减,且
上单调递减,且 ,
,如图∴sint=s在
 上有两个不同的解的充要条件是
上有两个不同的解的充要条件是 ,(12分)
,(12分)∴方程f(x)=m恰有两个不同的解的充要条件是
 .(14分)
.(14分)(注:单调区间写成
 、
、 也行;直接数形结合得到正确结果,也可)
也行;直接数形结合得到正确结果,也可)点评:本题考查的知识点是正弦型函数解析式的求法,三角方程的解法,正弦函数的图象和性质,其中(1)的关键是熟练掌握正弦型函数解析式中参数与函数性质的关系,(2)的关键是熟练掌握正弦型函数的性质,(3)的关键是将已知,结合正弦函数的性质,转化为一个关于m的不等式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
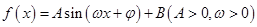 的一系列对应值如下表:
的一系列对应值如下表:







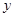



 的一个解析式;
的一个解析式; 周期为
周期为 ,当
,当 时,方程
时,方程 恰有两个不同的解,求实数
恰有两个不同的解,求实数 的取值范围.
的取值范围.  的一系列对应值如下表:
的一系列对应值如下表:






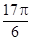



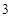
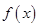 的一个解析式;
的一个解析式; 周期为
周期为 ,当
,当 时,方程
时,方程 恰有两个不同的解,求实数
恰有两个不同的解,求实数 的取值范围.
的取值范围.