在平面直角坐标系中，曲线与坐标轴的交点都在圆上．

(1)求圆的方程；

 (2)若圆与直线交于、两点，且，求的值．

【解析】本试题主要是考查了直线与圆的位置关系的运用。

（1）曲线与轴的交点为(0,1)，

与轴的交点为(3＋2，0)，(3－2，0) 故可设的圆心为(3，t)，则有3²＋(t－1)²＝(2)²＋t²，解得t＝1.

（2）因为圆与直线交于、两点，且。联立方程组得到结论。

求圆心在直线y＝－2x上，并且经过点A(2,－1)，与直线x＋y＝1相切的圆的方程.

【解析】利用圆心和半径表示圆的方程，首先

设圆心为S，则K_SA＝1,∴SA的方程为：y＋1＝x－2，即y＝x－3，  ………4分

和y＝－2x联立解得x＝1,y＝－2，即圆心(1,－2)  

∴r＝＝,

故所求圆的方程为：＋＝2

解：法一：

设圆心为S，则K_SA＝1,∴SA的方程为：y＋1＝x－2，即y＝x－3，  ………4分

和y＝－2x联立解得x＝1,y＝－2，即圆心(1,－2)             ……………………8分

∴r＝＝,                 ………………………10分

故所求圆的方程为：＋＝2                   ………………………12分

法二：由条件设所求圆的方程为：＋＝ 

 ,          ………………………6分

解得a＝1,b＝－2, ＝2                     ………………………10分

所求圆的方程为：＋＝2             ………………………12分

其它方法相应给分

．给出下列命题：

①命题“若b²－4ac<0，则方程ax²＋bx＋c＝0(a≠0)无实根”的否命题；

②命题在“△ABC中，AB＝BC＝CA，那么△ABC为等边三角形”的逆命题；

③命题“若a>b>0，则>>0”的逆否命题；

④若“m>1，则mx²－2(m＋1)x＋(m－3)>0的解集为R”的逆命题．

其中真命题的序号为________．

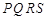如图，某小区准备绿化一块直径为的半圆形空地，外的地方种草，的内接正方形为一水池,其余地方种花.若 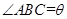,设的面积为，正方形的面积为，将比值称为“规划合理度”.

（1）试用,表示和.

（2）当为定值，变化时,求“规划合理度”取得最小值时的角的大小.

【解析】第一问中利用在ＡＢＣ中　　，

＝设正方形的边长为　　则  然后解得

第二问中，利用  而＝

借助于　为减函数 得到结论。 

（1）、 如图，在ＡＢＣ中　　，

＝　

设正方形的边长为　　则 

      ＝ 

（2）、  而＝  ∵0 <  < ,又0 <２ <,０<t£１　为减函数   

当时　取得最小值为此时　

已知直线x＋y－3m＝0和2x－y＋2m－1＝0的交点M在第四象限，求实数m的取值范围．

[分析]　解方程组得交点坐标，再根据点M在第四象限列出不等式组，解得m的取值范围．