摘要：--6' 当x＝1时.g(x)最小值＝g＝b--ln2.g(2)＝b-2+ln2 ∵方程f(x)+2x＝x2+b在[.2]上恰有两个不相等的实数根 由 Þ Þ +ln2≤b≤2 --9' (3)∵k-f(k)＝lnk ∴nk＝2 ó --10’ 设Φ(x)＝lnx-(x2-1) 则Φ'(x)＝-＝ 当x≥2时.Φ'(x)＜0 Þ 函数Φ上是减函数. ∴Φ＝ln2-＜0 Þ lnx＜(x2-1) --12' ∴当x≥2时. --13' ∴ ＞2[] ＝2(1+-) ＝. ∴原不等式成立. --14'
网址：http://m.1010jiajiao.com/timu_id_192234[举报]
| |||||||||||
(
、
分别是与x、y轴正半轴同方向的单位向量)，函数g(x)＝x2－x－6．
的最小值．设函数f(x)＝x4＋bx2＋cx＋d，当x＝t1时，f(x)有极小值．
(1)若b＝－6时，函数f（x）有极大值，求实数c的取值范围；
(2)在(1)的条件下，若存在实数c，使函数f(x)在闭区间［m－2，m＋2］上单调递增，求m的取值范围；
(3)若函数f(x)只有一个极值点，且存在t2∈(t1，t1＋1)，使f ′(t2)＝0，证明：函数g(x)＝f(x)－x2＋t1x在区间(t1，t2)内最多有一个零点．
查看习题详情和答案>>（本小题满分13分）(第一问8分，第二问5分)
已知函数f(x)＝2lnx，g(x)＝
ax2＋3x.
（1）设直线x＝1与曲线y＝f(x)和y＝g(x)分别相交于点P、Q，且曲线y＝f(x)和y＝g(x)在点P、Q处的切线平行，若方程f(x2＋1)＋g(x)＝3x＋k有四个不同的实根，求实数k的取值范围；
（2）设函数F(x)满足F(x)＋x［f′(x)－g′(x)］＝－3x2－(a＋6)x＋1.其中f′(x)，g′(x)分别是函数f(x)与g(x)的导函数；试问是否存在实数a，使得当x∈(0,1］时，F(x)取得最大值，若存在，求出a的取值范围；若不存在，说明理由.
查看习题详情和答案>>
ax2＋3x.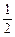
ax2＋3x.