网址：http://m.1010jiajiao.com/timu_id_192007[举报]
某个计算机有A，B两个数据输入口，另有C是计算结果的输出口，计算过程是由A，B分别输入正整数m和n．经计算得正整数k，然后由C输出(过程可简单表示为关系式f(m，n)＝k)．此种计算装置完成的计算机满足以下三个性质．
①若A，B的输入1，则输出的结果为2，即f(1，1)＝2；
②若A输入1，B的输入由n变为n＋1，则输出的结果比原来增大2，即f(1，n＋1)＝f(1，n)＋2；
③若B输入n，A的输入由m变为m＋1，则输出结果为原来的3倍，即f(m＋1，n)＝3f(m，n)．
试回答下列问题：
(1)若A输入2，B输入3，则输出结果为多少？
(2)若A输入1，B输入n(n∈N+)，则输出结果为多少？
(3)由C能输出多少个不同的两位数？
说明：本题题干比较长，情景相对陌生，将题干中的语言转化为数列语言是解题关键．
⊙O1和⊙O2的极坐标方程分别为
，
．
⑴把⊙O1和⊙O2的极坐标方程化为直角坐标方程；
⑵求经过⊙O1，⊙O2交点的直线的直角坐标方程．
【解析】本试题主要是考查了极坐标的返程和直角坐标方程的转化和简单的圆冤啊位置关系的运用
（1）中，借助于公式
，
，将极坐标方程化为普通方程即可。
（2）中，根据上一问中的圆的方程，然后作差得到交线所在的直线的普通方程。
解：以极点为原点，极轴为x轴正半轴，建立平面直角坐标系，两坐标系中取相同的长度单位．
(I)，，由得
．所以
．
即
为⊙O1的直角坐标方程．
同理
为⊙O2的直角坐标方程．
(II)解法一:由
解得
，
即⊙O1，⊙O2交于点(0,0)和(2,－2)．过交点的直线的直角坐标方程为y=－x．
解法二: 由,两式相减得－4x-4y=0,即过交点的直线的直角坐标方程为y=－x
查看习题详情和答案>>
已知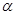
为第三象限角，
．
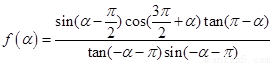（１）化简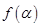
（２）若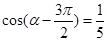
，求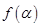的值 （本小题满分10分）
【解析】第一问利用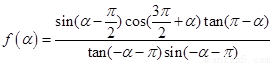
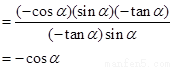
第二问∵ ∴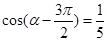 
从而
，从而得到三角函数值。
解：（1）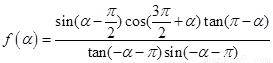
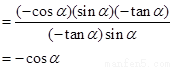
（2）∵
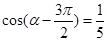
∴ 从而 ………………………8分
又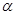为第三象限角
∴
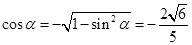………………………10分
即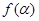
的值为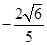
查看习题详情和答案>>
水车是一种利用水流的动力进行灌溉的工具，图1-6-5是一个水车的示意图，它的直径为3 m，其中心(即圆心)O距水面1.2 m.如果水车每4 min逆时针转3圈，在水车轮边缘上取一点P，我们知道在水车匀速转动时，P点距水面的高度h(m)是一个变量，显然，它是时间t(s)的函数.我们知道，h与t的函数关系反映了这个周期现象的规律.为了方便，不妨从P点位于水车与水面交点Q时开始记时(t=0).
首先，设法用解析式表示出这个函数关系，并用“五点法”作出这个函数在一个周期内的简图.
图1-6-5
其次，我们讨论如果雨季河水上涨或旱季河流水量减少时，所求得的函数解析式中的参数将发生哪些变化？若水车转速加快或减慢，函数解析式中的参数又会受到怎样的影响？
查看习题详情和答案>>水车问题．
水车是一种利用水流的动力进行灌溉的工具，下图是一个水车的示意图，它的直径为3 m，其中心(即圆心)O距水面1.2 m．如果水车每4 min逆时针转3圈，在水车轮边缘上取一点P，我们知道在水车匀速转动时，P点距水面的高度h(m)是一个变量，显然，它是时间t(s)的函数．我们知道，h与t的函数关系反映了这个周期现象的规律．为了方便，不妨从P点位于水车与水面交点Q时开始记时(t＝0)．
首先，设法用解析式表示出这个函数关系，并用“五点法”作出这个函数在一个周期内的简图．
其次，我们讨论如果雨季河水上涨或旱季河流水量减少时，所求得的函数解析式中的参数将发生哪些变化？若水车转速加快或减慢，函数解析式中的参数又会受到怎样的影响？