摘要:(3)可以计算得到. .
网址:http://m.1010jiajiao.com/timu_id_191741[举报]
利用计算机随机模拟方法计算y=x2与y=4所围成的区域Ω的面积时,可以先运行以下算法步骤:
第一步:利用计算机产生两个在[0,1]区间内的均匀随机数a,b;
第二步:对随机数a,b实施变换:
得到点A(a1,b1);
第三步:判断点A(a1,b1)的坐标是否满足b1<
;
第四步:累计所产生的点A的个数m,及满足b1<
的点A的个数n;
第五步:判断m是否小于M(一个设定的数).若是,则回到第一步,否则,输出n并终止算法.
若设定的M=100,且输出的n=34,则据此用随机模拟方法可以估计出区域Ω的面积为 (保留小数点后两位数字).
查看习题详情和答案>>
第一步:利用计算机产生两个在[0,1]区间内的均匀随机数a,b;
第二步:对随机数a,b实施变换:
|
第三步:判断点A(a1,b1)的坐标是否满足b1<
| a | 2 1 |
第四步:累计所产生的点A的个数m,及满足b1<
| a | 2 1 |
第五步:判断m是否小于M(一个设定的数).若是,则回到第一步,否则,输出n并终止算法.
若设定的M=100,且输出的n=34,则据此用随机模拟方法可以估计出区域Ω的面积为
利用计算机随机模拟方法计算y=x2与y=9所围成的区域Ω的面积时,可以先运行以下算法步骤:
第一步:利用计算机产生两个在0~1区间内的均匀随机数a,b;
第二步:对随机数a,b实施变换:
得到点A(a1,b1);
第三步:判断点A(a1,b1)的坐标是否满足b1<
;
第四步:累计所产生的点A的个数m,及满足b1<
的点A的个数n;
第五步:判断m是否小于M(一个设定的数).若是,则回到第一步,否则,输出n并终止算法.
(1)点落在y=x2上方的概率计算公式是P= ;
(2)若设定的M=1000,且输出的n=340,则用随机模拟方法可以估计出区域Ω的面积为 (保留小数点后两位数字).
查看习题详情和答案>>
第一步:利用计算机产生两个在0~1区间内的均匀随机数a,b;
第二步:对随机数a,b实施变换:
|
第三步:判断点A(a1,b1)的坐标是否满足b1<
| a | 2 1 |
第四步:累计所产生的点A的个数m,及满足b1<
| a | 2 1 |
第五步:判断m是否小于M(一个设定的数).若是,则回到第一步,否则,输出n并终止算法.
(1)点落在y=x2上方的概率计算公式是P=
(2)若设定的M=1000,且输出的n=340,则用随机模拟方法可以估计出区域Ω的面积为
利用计算机随机模拟方法计算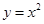 与
与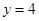 所围成的区域
所围成的区域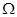 的面积时,可以先运行以下算法步骤:
的面积时,可以先运行以下算法步骤:
第一步:利用计算机产生两个在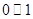 区间内的均匀随机数
区间内的均匀随机数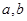 ;
;
第二步:对随机数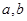 实施变换:
实施变换: 得到点
得到点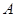
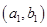 ;
;
第三步:判断点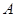
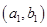 的坐标是否满足
的坐标是否满足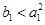 ;
;
第四步:累计所产生的点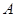 的个数
的个数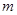 ,及满足
,及满足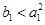 的点
的点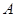 的个数
的个数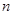 ;
;
第五步:判断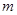 是否小于
是否小于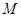 (一个设定的数).若是,则回到第一步,否则,输出
(一个设定的数).若是,则回到第一步,否则,输出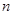 并终止算法.
并终止算法.
若设定的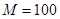 ,且输出的
,且输出的 ,则据此用随机模拟方法可以估计出区域
,则据此用随机模拟方法可以估计出区域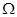 的面积为
的面积为
(保留小数点后两位数字).
查看习题详情和答案>>
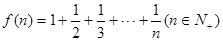 .经计算得
.经计算得 ,
,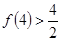 ,
,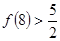 ,
,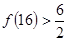 ,
,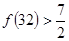 ,通过观察,我们可以得到一个一般性的结论.
,通过观察,我们可以得到一个一般性的结论.  ,试问是否存在正整数
,试问是否存在正整数 ,使得
,使得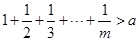 ?
?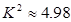 ,那么可以得到的结
,那么可以得到的结