题目内容
利用计算机随机模拟方法计算y=x2与y=9所围成的区域Ω的面积时,可以先运行以下算法步骤:第一步:利用计算机产生两个在0~1区间内的均匀随机数a,b;
第二步:对随机数a,b实施变换:
|
第三步:判断点A(a1,b1)的坐标是否满足b1<
| a | 2 1 |
第四步:累计所产生的点A的个数m,及满足b1<
| a | 2 1 |
第五步:判断m是否小于M(一个设定的数).若是,则回到第一步,否则,输出n并终止算法.
(1)点落在y=x2上方的概率计算公式是P=
(2)若设定的M=1000,且输出的n=340,则用随机模拟方法可以估计出区域Ω的面积为
分析:(1)由第三步可知,n表示y=x2下方的点A的个数,其概率为
,故可求点落在y=x2上方的概率;
(2)先由计算器做模拟试验结果试验估计,得出点落在阴影部分的点的概率,再转化为几何概型的面积类型求解阴影部分的面积S.
| n |
| M |
(2)先由计算器做模拟试验结果试验估计,得出点落在阴影部分的点的概率,再转化为几何概型的面积类型求解阴影部分的面积S.
解答:解:(1)由第三步可知,n表示y=x2下方的点A的个数,其概率为
,故点落在y=x2上方的概率为1-
;
(2)由(1)知,P=1-
=0.66,矩形的面积为9×6=54,
设阴影部分的面积为S,则有
=0.66,
∴S=54×0.66=35.64.
故答案为:1-
;35.64.
| n |
| M |
| n |
| M |
(2)由(1)知,P=1-
| 340 |
| 1000 |
设阴影部分的面积为S,则有
| S |
| 54 |
∴S=54×0.66=35.64.
故答案为:1-
| n |
| M |
点评:本题考查模拟方法估计概率以及几何概型中面积类型,考查学生的计算能力,属于中档题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
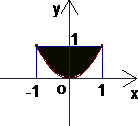 利用计算机随机模拟方法计算图中阴影面积(如图所示)
利用计算机随机模拟方法计算图中阴影面积(如图所示)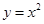 与
与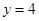 所围成的区域
所围成的区域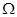 的面积时,可以先运行以下算法步骤:
的面积时,可以先运行以下算法步骤: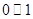 区间内的均匀随机数
区间内的均匀随机数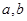 ;
; 得到点
得到点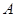
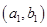 ;
;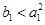 ;
;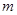 ,及满足
,及满足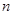 ;
;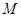 (一个设定的数).若是,则回到第一步,否则,输出
(一个设定的数).若是,则回到第一步,否则,输出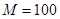 ,且输出的
,且输出的 ,则据此用随机模拟方法可以估计出区域
,则据此用随机模拟方法可以估计出区域