摘要：(i)当2-a=0即a=2时.无极值.舍去.
网址：http://m.1010jiajiao.com/timu_id_191714[举报]
（2012•海淀区二模）已知函数f(x)=aln(x-a)-
x2+x(a＜0)．
（I）当-1＜a＜0时，求f（x）的单调区间；
（II）若-1＜a＜2（ln2-1），求证：函数f（x）只有一个零点x0，且a+1＜x0＜a+2；
（III）当a=-
时，记函数f（x）的零点为x0，若对任意x1，x2∈[0，x0]且x2-x1=1，都有|f（x2）-f（x1）|≥m成立，求实数m的最大值．
（本题可参考数据：ln2=0.7，ln
=0.8，ln
=0.59）
查看习题详情和答案>>
| 1 |
| 2 |
（I）当-1＜a＜0时，求f（x）的单调区间；
（II）若-1＜a＜2（ln2-1），求证：函数f（x）只有一个零点x0，且a+1＜x0＜a+2；
（III）当a=-
| 4 |
| 5 |
（本题可参考数据：ln2=0.7，ln
| 9 |
| 4 |
| 9 |
| 5 |
在平面直角坐标系中，已知矩形ABCD的长为2，宽为1，AB、AD边分别在x轴、y轴的正半轴上，A点与坐标原点重合（如图）．将矩形折叠，使A点落在线段DC上．（I）若折痕所在直线的斜率为k，试求折痕所在直线的方程；
（II）当-2+
| 3 |
（Ⅲ）当-2≤k≤-1时，折痕为线段PQ，设t=k（2|PQ|2-1），试求t的最大值．
椭圆
+
=1(a＞b＞0)的左、右焦点分别为F1、F2，点P在椭圆上，∠F1PF2=60°，设
=λ
（I）当λ=2时，求椭圆离心率e；
（II）当椭圆离心率最小时，PQ为过椭圆右焦点F2的弦，且|PQ|=
，求椭圆的方程．
查看习题详情和答案>>
| x2 |
| a2 |
| y2 |
| b2 |
| |PF1| |
| |PF2| |
（I）当λ=2时，求椭圆离心率e；
（II）当椭圆离心率最小时，PQ为过椭圆右焦点F2的弦，且|PQ|=
| 16 |
| 5 |
．
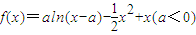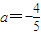时，记函数f（x）的零点为x，若对任意x1，x2∈[0，x]且x2-x1=1，都有|f（x2）-f（x1）|≥m成立，求实数m的最大值．
，
）
．
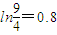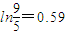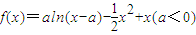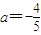时，记函数f（x）的零点为x，若对任意x1，x2∈[0，x]且x2-x1=1，都有|f（x2）-f（x1）|≥m成立，求实数m的最大值．
，
）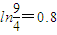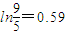