网址:http://m.1010jiajiao.com/timu_id_18586[举报]
一、选择题(本题有12小题,共48分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
C
B
A
C
D
A
B
A
C
B
D
二、填空题(本大题为选做题,在8小题中做对6小题即得满分30分,多做答错不扣分)
13. 2 14. 15. 16.答案不唯一,比如等
17.70° 18.10、30 19.1476.5 20. +、1
三、解答题(本题有7小题,共72分)
说明:本参考答案中除25、27题外每题只给出了一种解答,对于其他解答,只要解法正确,参照本评分建议给分。
21. 解:原方程变形得:, ………………………………2分
. ……………………………………………4分
∴ 方程的根为:、 、 . …………………………8分
22.(1)∠ABC= 135 °, ………………………………………………………2分
BC=; …………………………………………………………4分
(2)能判断△ABC与△DEF相似(或△ABC∽△DEF) ………………5分
这是因为∠ABC =∠DEF = 135 ° ,,
∴△ABC∽△DEF. …………………………………………8分
23. (1) 在这组数据中,中位数是30.0 , ……………………………………2分
众数是30.0 , …………………………………………………4分
平均数是32.0 ; ……………………………………6分
(若填为30、30、32,均暂不扣分)
(2) 凭经验,大厦高约30.0 .(单位未写暂不扣分) …………………7分
只要说得有理就给1分,比如数据44.0误差太大,或测量错误不可信等等.8分
24. 解:在R t△BCD中,∵ BD=5, ∴ BC=5= 4.1955≈4.20. ……4分
在R t△BCD中,BE=BC+CE= 6.20, …………………………………5分
∴ DE= ……………………………………………6分
==
≈7.96 ……………………………………………………………9分
答:BC的长度约为4.20,钢缆ED的长度约7.96. …………………10分
(若BC=4.1955暂不扣分,但是ED的长度未保留三个有效数字扣1分)
25. 解:(1) 由已知,矩形的另一边长为 ………………………………1分
则= ……………………………………………………3分
= ……………………………………………………………5分
自变量的取值范围是0<<18. ……………………7分
(2)∵ == …………………………………10分
∴ 当=9时(0<9<18),苗圃的面积最大 ……………………11分
最大面积是81 ………………………………………………12分
又解: ∵ =-1<0,有最大值, …………………………8分
∴ 当 =时(0<9<18), ………………………10分
() ……………………………12分
(未指出0<9<18暂不扣分)
26. 解:(1) ……………………………1分
; ………………………3分
又 , ……………………………………4分
∴ . …6分
⑵…8分
………………10分
……………………………………11分
∴ …12分
(说明:若在整个推导过程中,始终带根号运算当然也正确。)
27.解: ⑴ C(5,-4);(过程1分,纵、横坐标答对各得1分) ………… 3分
⑵ 能 ……………………………………………………………4分
连结AE ,∵BE是⊙O的直径, ∴∠BAE=90°. ………5分
在△ABE与△PBA中,AB2=BP? BE , 即, 又∠ABE=∠PBA,
∴△ABE∽△PBA . …………………………………7分
∴∠BPA=∠BAE=90°, 即AP⊥BE . …………………8分
⑶ 分析:假设在直线EB上存在点Q,使AQ2=BQ? EQ. Q点位置有三种情况:
①若三条线段有两条等长,则三条均等长,于是容易知点C即点Q;
②若无两条等长,且点Q在线段EB上,由Rt△EBA中的射影定理知点Q即为AQ⊥EB之垂足;
③若无两条等长,且当点Q在线段EB外,由条件想到切割线定理,知QA切⊙C于点A.设Q(),并过点Q作QR⊥x轴于点R,由相似三角形性质、切割线定理、勾股定理、三角函数或直线解析式等可得多种解法.
解题过程:
① 当点Q1与C重合时,AQ1=Q1B=Q1E, 显然有AQ12=BQ1? EQ1 ,
∴Q1(5, -4)符合题意; ………………………………9分
② 当Q2点在线段EB上, ∵△ABE中,∠BAE=90°
∴点Q2为AQ2在BE上的垂足, ………………………10分
∴AQ2== 4.8(或).
∴Q2点的横坐标是2+ AQ2?∠BAQ2= 2+3.84=5.84,
又由AQ2?∠BAQ2=2.88,
∴点Q2(5.84,-2.88), …………11分
③方法一:若符合题意的点Q3在线段EB外,
则可得点Q3为过点A的⊙C的切线与直线BE在第一象限的交点.
由Rt△Q3BR∽Rt△EBA,△EBA的三边长分别为6、8、10,
故不妨设BR=3t,RQ3=4t,BQ3=5t, …………………………12分
由Rt△ARQ3∽Rt△EAB得, ………………………13分
即得t=,
〖注:此处也可由列得方程; 或由AQ32 = Q3B?Q3E=Q3R2+AR2列得方程)等等〗
∴Q3点的横坐标为8+3t=, Q3点的纵坐标为,
即Q3(,) . ……………………14分
方法二:如上所设与添辅助线, 直线 BE过B(8, 0), C(5, -4),
∴直线BE的解析式是. ……………12分
设Q3(,),过点Q3作Q3R⊥x轴于点R,
∵易证∠Q3AR =∠AEB得 Rt△AQ3R∽Rt△EAB,
∴, 即 , ………………13分
∴t=,进而点Q3 的纵坐标为,∴Q3(,). ………14分
方法三:若符合题意的点Q3在线段EB外,连结Q3A并延长交轴于F,
∴∠Q3AB =∠Q3EA,,
在R t△OAF中有OF=2×=,点F的坐标为(0,),
∴可得直线AF的解析式为, ………………12分
又直线BE的解析式是, ………………13分
∴可得交点Q3(,). ………………………14分
现有7名同学测得某大厦的高度如下:(单位: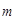 )29.8 30.0 30.0 30.0 30.2 44.0 30.0
)29.8 30.0 30.0 30.0 30.2 44.0 30.0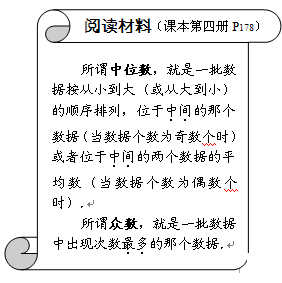
(1) 在这组数据中,中位数是 , 众数是 ,平均数是 ;
(2) 凭经验,你觉得此大厦大概有多高?请简要说明理由.
现有7名同学测得某大厦的高度如下:(单位: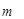 )29.8 30.0 30.0 30.0
30.2 44.0 30.0
)29.8 30.0 30.0 30.0
30.2 44.0 30.0

(1) 在这组数据中,中位数是 , 众数是 ,平均数是 ;
(2) 凭经验,你觉得此大厦大概有多高?请简要说明理由.
查看习题详情和答案>>
 )29.8 30.0 30.0 30.0 30.2 44.0 30.0
)29.8 30.0 30.0 30.0 30.2 44.0 30.0
(1) 在这组数据中,中位数是 , 众数是 ,平均数是 ;
(2) 凭经验,你觉得此大厦大概有多高?请简要说明理由.
