摘要:解:(1)如图建系.设椭圆方程为,则
网址:http://m.1010jiajiao.com/timu_id_183526[举报]
(2012•武昌区模拟)为美化环境,某地决定在一个大型广场建一个同心圆形花坛,花坛分为两部分,中间小圆部分种植草坪,周围的圆环分为n(n≥3,n∈N)等份种植红、黄、蓝三色不同的花.要求相邻两部分种植不同颜色的花.如图①,圆环分成的3等份分别为a1,a2,a3,有6种不同的种植方法.

(1)如图②,圆环分成的4等份分别为 a1,a2,a3,a4,有
(2)如图③,圆环分成的n(n≥3,n∈N)等份分别为a1,a2,a3,…,an,有
查看习题详情和答案>>

(1)如图②,圆环分成的4等份分别为 a1,a2,a3,a4,有
18
18
种不同的种植方法;(2)如图③,圆环分成的n(n≥3,n∈N)等份分别为a1,a2,a3,…,an,有
2n-2•(-1)n-3(n≥3且n∈N)
2n-2•(-1)n-3(n≥3且n∈N)
种不同的种植方法.
如图,实线部分的月牙形公园是由圆P上的一段优弧和圆Q上的一段劣弧围成,圆P和圆Q的半径都是2km,点P在圆Q上,现要在公园内建一块顶点都在圆P上的多边形活动场地.
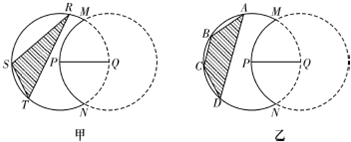
(1)如图甲,要建的活动场地为△RST,求场地的最大面积;
(2)如图乙,要建的活动场地为等腰梯形ABCD,求场地的最大面积. 查看习题详情和答案>>

(1)如图甲,要建的活动场地为△RST,求场地的最大面积;
(2)如图乙,要建的活动场地为等腰梯形ABCD,求场地的最大面积. 查看习题详情和答案>>
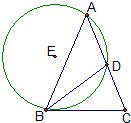 (1)如图,在△ABC中,AB=AC,∠C=72°,⊙E过A,B两点且与BC相切于点B,与AC交于点D,连接BD,若BC=
(1)如图,在△ABC中,AB=AC,∠C=72°,⊙E过A,B两点且与BC相切于点B,与AC交于点D,连接BD,若BC=| 5 |
(2)过点A(2,3)的直线的参数方程为
|
(3)若关于x的不等式x+|x-1|≤a无解,则实数a的取值范围为
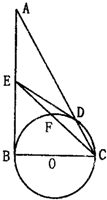 (选修4-1)如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,设E为AB的中点.
(选修4-1)如图,在△ABC中,∠ABC=90°,以BC为直径的圆O交AC于点D,设E为AB的中点. (I)求证:直线DE为圆O的切线;
(Ⅱ)设CE交圆O于点F,求证:CD•CA=CF•CE
(选修4-4)在平面直角坐标系xoy中,圆C的参数方程为
|
| π |
| 3 |
(I)写出圆C的标准方程和直线l的参数方程;
(Ⅱ)设直线l与圆C相交于A,B两点,求|PA|-|PB|的值.
(选修4-5)已知函数f(x)=|2x+1|,g(x)=|x|+a
(Ⅰ)当a=0时,解不等式f(x)≥g(x);
(Ⅱ)若存在x∈R,使得f(x)≤g(x)成立,求实数a的取值范围.
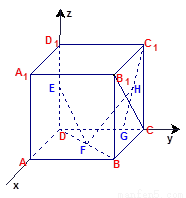
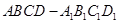 中,
中,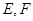 分别是
分别是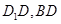 的中点,
的中点,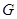 在棱
在棱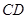 上,且
上,且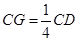 ,H为
,H为 的中点,应用空间向量方法求解下列问题.
的中点,应用空间向量方法求解下列问题.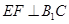 ;
;