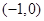摘要：当且仅当.即时等号成立．当时..
网址：http://m.1010jiajiao.com/timu_id_182753[举报]
23、课本小结与复习的参考例题中，给大家分别用“综合法”，“比较法”和“分析法”证明了不等式：已知a，b，c，d都是实数，且a2+b2=1，c2+d2=1，则|ac+bd|≤1．这就是著名的柯西（Cauchy．法国）不等式当n=2时的特例，即（ac+bd）2≤（a2+b2）（c2+d2），等号当且仅当ad=bc时成立．
请分别用中文语言和数学语言简洁地叙述柯西不等式，并用一种方法加以证明．
查看习题详情和答案>>
请分别用中文语言和数学语言简洁地叙述柯西不等式，并用一种方法加以证明．
课本小结与复习的参考例题中，给大家分别用“综合法”，“比较法”和“分析法”证明了不等式：已知a，b，c，d都是实数，且a2+b2=1，c2+d2=1，则|ac+bd|≤1．这就是著名的柯西（Cauchy．法国）不等式当n=2时的特例，即（ac+bd）2≤（a2+b2）（c2+d2），等号当且仅当ad=bc时成立．
请分别用中文语言和数学语言简洁地叙述柯西不等式，并用一种方法加以证明．
查看习题详情和答案>>
请分别用中文语言和数学语言简洁地叙述柯西不等式，并用一种方法加以证明．
课本小结与复习的参考例题中，给大家分别用“综合法”，“比较法”和“分析法”证明了不等式：已知a，b，c，d都是实数，且a2+b2=1，c2+d2=1，则|ac+bd|≤1．这就是著名的柯西（Cauchy．法国）不等式当n=2时的特例，即（ac+bd）2≤（a2+b2）（c2+d2），等号当且仅当ad=bc时成立．
请分别用中文语言和数学语言简洁地叙述柯西不等式，并用一种方法加以证明．
查看习题详情和答案>>
请分别用中文语言和数学语言简洁地叙述柯西不等式，并用一种方法加以证明．
查看习题详情和答案>>
设向量
=（a，b），
=（m，n），其中a，b，m，n∈R，由不等式|
•
|≤|
|•|
|恒成立，可以证明（柯西）不等式（am+bn）2≤（a2+b2）（m2+n2）（当且仅当
∥
，即an=bm时等号成立），己知x，y∈R+，若
+3
＜k•
恒成立，利用柯西不等式可求得实数k的取值范围是 ．
查看习题详情和答案>>
| α |
| β |
| α |
| β |
| α |
| β |
| α |
| β |
| x |
| y |
| x+y |
已知函数
其中
为自然对数的底数，
.(Ⅰ)设
，求函数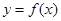
的最值；（Ⅱ）若对于任意的
，都有
成立，求
的取值范围.
【解析】第一问中，当
时，
，
．结合表格和导数的知识判定单调性和极值，进而得到最值。
第二问中，∵
，
，
∴原不等式等价于：
,
即
, 亦即
分离参数的思想求解参数的范围
解：（Ⅰ)当时，，．
当在
上变化时，
，
的变化情况如下表：
|
|
|
|
|
|
|
|
|
|
－ |
|
＋ |
|
|
|
|
|
|
|
1／e |
∴
时，
，
．
(Ⅱ)∵，，
∴原不等式等价于：
,
即, 亦即．
∴对于任意的
，原不等式恒成立,等价于对
恒成立,
∵对于任意的时, 
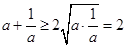（当且仅当
时取等号）．
∴只需
，即
，解之得
或
.
因此，的取值范围是
查看习题详情和答案>>