摘要：(2)由＝λ.∴λ+1＝4.λ＝3 或O点与P点重合= 7′当O点与P点重合=时.m=0当λ＝3时.直线l与y轴相交.则斜率存在.设l与椭圆C交点为A(x1.y1).B(x2.y2) 得(k2+2)x2+2kmx+(m2-1)＝0Δ＝(2km)2-4(k2+2)(m2-1)＝4(k2-2m2+2)＞0 (*)x1+x2＝. x1x2＝ 11′∵＝3 ∴-x1＝3x2 ∴消去x2.得3(x1+x2)2+4x1x2＝0.∴3()2+4＝0整理得4k2m2+2m2-k2-2＝0 13′m2＝时.上式不成立,m2≠时.k2＝.因λ＝3 ∴k≠0 ∴k2＝＞0.∴-1＜m＜- 或 ＜m＜1容易验证k2＞2m2-2成立.所以(*)成立即所求m的取值范围为∪{0} 16′
网址：http://m.1010jiajiao.com/timu_id_182639[举报]
对变量x，y有观测数据(xi，yi)(i＝1,2，…，10)，得散点图1；对变量u，v有观测数据(ui，vi)(i＝1,2，…，10)，得散点图2．由这两个散点图可以判断( )
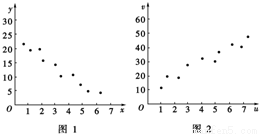
A．变量x与y正相关，u与v正相关
B．变量x与y正相关，u与v负相关
C．变量x与y负相关，u与v负相关
D．变量x与y负相关，u与v正相关
查看习题详情和答案>>
如图，几何体ABC一EFD是由直三棱柱截得的，EF //AB，∠ABC＝90°，AC＝2AB = 2.，CD＝2AE＝
（I）求三棱锥。D－BES的体积；
（B）求证：CE⊥DB
查看习题详情和答案>>
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截面得，已知FA⊥平面ABC，AB＝2，BD＝1，AF＝2， CE＝3，O为AB的中点．
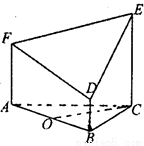
（1）求证：OC⊥DF；
（2）求平面DEF与平面ABC相交所成锐二面角的大小；
（3）求多面体ABC—FDE的体积V．
查看习题详情和答案>>
)的图象的一个最高点为(2,2
)，由这个最高点到相邻最低点，图象与x轴交于(6,0)点，试求这个函数的解析式．