网址：http://m.1010jiajiao.com/timu_id_174610[举报]
一、单项选择题
1、B 2、A 3、C 4、B 5、A
二、多项选择题
6、ABD 7、BD 8、BCD 9、BD
三、简答题
10、⑴60； ⑵7.18； ⑶3.59
11、（1）0.1s内放电的电量 （2分） （2）5.52×10
（3）6.9×10
12、（1）
实验原理图（图略）：电流表外接法（2分） 滑动变阻器为限流器 （2分）
（2）半导体 （2分）
（3）右 （2分） t=
四、论述计算题
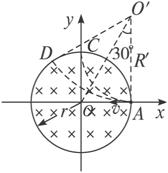
13、（12分）（1）由粒子的飞行轨迹，利用左手定则可知，该粒子带负电荷。
粒子由 A点射入，由
C点飞出，其速度方向改变了 90°，则粒子轨迹半径
1
又 
2
则粒子的比荷 
3
（2）粒子从 D 点飞出磁场速度方向改变了 60°角，故
AD 弧所对圆心角 60°，粒子做圆周运动的半径
4
又
5
所以 
6
粒子在磁场中飞行时间
7
14、（14分）解：（1）、（2）设：小球在C点的速度大小是Vc，对轨道的压力大小为NC，则对于小球由A→C的过程中，应用动能定律列出：
…………………①
在C点的圆轨道径向应用牛顿第二定律，有：
……………………………②
解得：
………③
…………………………④
∴小球的最大能动EKM：
………………………………………………⑥
（1分），
（1分）
（1分），
№
（1分）
（1分）， 
。 
（1分），
（1分），
（1分）， 
（1分）。
应将R调至10Ω。
洛仑兹力提供向心力
，由几何关系：
，求出
，垂直纸面向里。 电子做匀速直线运动
， 求出
，沿
轴负方向。
（2）只有电场时，电子从MN上的D点离开电场，如答图2所示，设D点横坐标为
，
， 
，求出D点的横坐标为
，纵坐标为
。
，求出
。
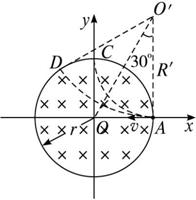
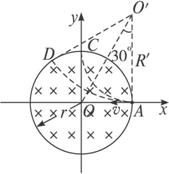
在以坐标原点O为圆心、半径为r的圆形区域内，存在磁感应强度大小为B、方向垂直于纸面向里的匀强磁场，如图所示．一个不计重力的带电粒子从磁场边界与x轴的交点A处以速度v沿-x方向射入磁场，恰好从磁场边界与y轴的交点C处沿+y方向飞出．
;
