摘要：4．注意代换后参数的等价性例8已知y＝2sinθcosθ+sinθ-cosθ(0≤θ≤π).求y的最大值.最小值解:设t＝sinθ-cosθ＝sin(θ-)∴2sinθcosθ＝1-t2∴y＝-t2+t+1＝-(t-)2+又∵t＝sin(θ-).0≤θ≤π 教 学 过 程组织教学 导入新课 讲授新课 归纳小结 布置作业 ∴-≤θ-≤∴-1≤t≤当t＝时.ymax＝当t＝-1时.ymin＝-1说明:此题在代换中.据θ范围.确定了参数t∈［-1.］.从而正确求解.若忽视这一点.会发生t＝时有最大值而无最小值的结论五.课后作业:六.板书设计(略)七.课后记:
网址：http://m.1010jiajiao.com/timu_id_170308[举报]
（1）选修4-4：矩阵与变换
已知曲线C1：y=
绕原点逆时针旋转45°后可得到曲线C2：y2-x2=2，
（I）求由曲线C1变换到曲线C2对应的矩阵M1；
（II）若矩阵M2=
，求曲线C1依次经过矩阵M1，M2对应的变换T1，T2变换后得到的曲线方程．
（2）选修4-4：坐标系与参数方程
已知直线l的极坐标方程是ρcosθ+ρsinθ-1=0．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，在曲线C：
（θ为参数）上求一点，使它到直线l的距离最小，并求出该点坐标和最小距离．
（3）（选修4-5：不等式选讲）
将12cm长的细铁线截成三条长度分别为a、b、c的线段，
（I）求以a、b、c为长、宽、高的长方体的体积的最大值；
（II）若这三条线段分别围成三个正三角形，求这三个正三角形面积和的最小值．
查看习题详情和答案>>
已知曲线C1：y=
| 1 |
| x |
（I）求由曲线C1变换到曲线C2对应的矩阵M1；
（II）若矩阵M2=
|
（2）选修4-4：坐标系与参数方程
已知直线l的极坐标方程是ρcosθ+ρsinθ-1=0．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，在曲线C：
|
（3）（选修4-5：不等式选讲）
将12cm长的细铁线截成三条长度分别为a、b、c的线段，
（I）求以a、b、c为长、宽、高的长方体的体积的最大值；
（II）若这三条线段分别围成三个正三角形，求这三个正三角形面积和的最小值．
（2009•黄浦区一模）如图所示，点A、B是单位圆（圆心在原点，半径为1的圆）上两点，OA、OB与x轴正半轴所成的角分别为α和-β．记| OA |
| OB |
| OA |
| OB |
cos（α+β）=cosαcosβ-sinαsinβ
cos（α+β）=cosαcosβ-sinαsinβ
．
已知圆C的参数方程是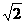
(α为参数)和直线l对应的普通方程是x-y-6
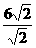=0.
(α为参数)和直线l对应的普通方程是x-y-6=0.(1)如果把圆心平移到原点O，请问平移后圆和直线满足什么关系?
(2)写出平移后圆的摆线方程.
(3)求摆线和x轴的交点.
查看习题详情和答案>>
(α为参数)和直线l对应的普通方程是x-y-
=0.
(α为参数)和直线l对应的普通方程是x-y-6
=0.