网址:http://m.1010jiajiao.com/timu_id_164100[举报]
1、D 2、C 3、C 4、C 5、B 6、C
7、4 8、 9、
9、 10、
10、 
11、解:(Ⅰ) ∵ 底面ABCD是正方形,
∵ 底面ABCD是正方形,
∴AB⊥BC,
又平面PBC⊥底面ABCD
平面PBC ∩ 平面ABCD=BC
∴AB ⊥平面PBC
又PC 平面PBC
平面PBC
∴AB ⊥CP ………………3分
(Ⅱ)解法一:体积法.由题意,面 面
面 ,
,
取 中点
中点 ,则
,则
 面
面 .
.
再取 中点
中点 ,则
,则 ………………5分
………………5分
设点 到平面
到平面 的距离为
的距离为 ,则由
,则由



 .
………………7分
.
………………7分
 解法二:
解法二: 面
面
取 中点
中点 ,再取
,再取 中点
中点

 ,
,


过点 作
作 ,则
,则
在 中,
中,
由
∴点 到平面
到平面 的距离为
的距离为 。 ………………7分
。 ………………7分
(Ⅲ)
 面
面


 就是二面角
就是二面角 的平面角.
的平面角.


∴二面角 的大小为45°. ………………12分
的大小为45°. ………………12分
12、解:(I)证明:在直棱柱ABC-A1B
∵
∠ACB=90º,∴A
∵CG 平面C1CBB1,∴A
平面C1CBB1,∴A
在矩形C1CBB1中,CC1=BB1=2BC,G为BB1的中点,
CG= BC,C
BC,C BC,CC1=2BC
BC,CC1=2BC
∴∠CGC1=90,即CG⊥C
而A
∴CG⊥平面A1GC1。
∴平面A1CG⊥平面A1GC1。┉┉┉┉┉┉┉┉6分
(II)由于CC1平面ABC,
∠ACB=90º,建立如图所示的空间坐标系,设AC=BC=CC1=a,则A(a,0,0),B(0,a,0)
A1(a,0,
∴ =(a,0,
=(a,0, =(0,a,a). ┉┉┉┉┉┉┉┉8分
=(0,a,a). ┉┉┉┉┉┉┉┉8分
设平面A1CG的法向量n1=(x1,y1,z1),
由 得
得
令z1=1,n1=(-2,-1,1). ┉┉┉┉┉┉┉┉9分
又平面ABC的法向量为n2=(0,0,1) ┉┉┉┉┉┉┉┉10分
设平面ABC与平面A1CG所成锐二面角的平面角为θ,
则 ┉┉┉┉┉┉┉┉11分
┉┉┉┉┉┉┉┉11分
即平面ABC与平面A1CG所成锐二面角的平面角的余弦值为 。┉┉┉12分
。┉┉┉12分
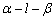 的大小为
的大小为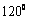 ,
,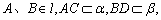
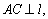
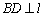 ,
,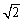 B.4 C.2
B.4 C.2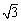 D.2
D.2