Question

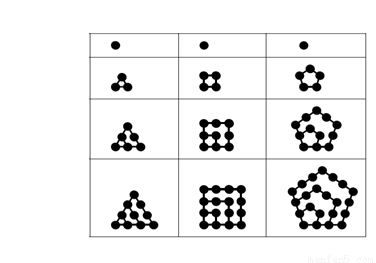
用大小一样的钢珠可以排成正三角形、正方形与正五边形数组，其排列的规律如下图所示：
已知m个钢珠恰好可以排成每边n个钢珠的正三角形数组与正方形数组各一个；且知若用这m个钢珠去排成每边n个钢珠的正五边形数组时，就会多出9个钢珠，则m=

 

．

Answer 1

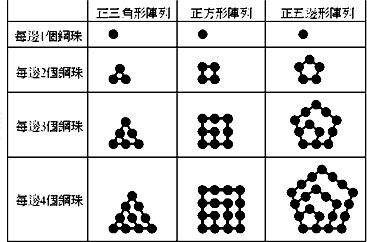
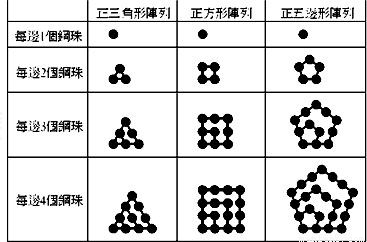
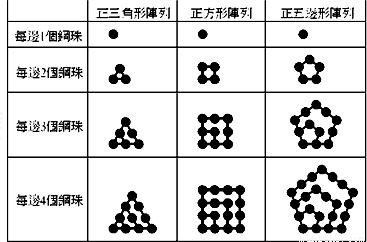
分析：根据所给的图形观察图形的特点，边上每增加一个珠子时，组成正多边形的珠子数的变化规律，得到三个等差数列，根据等差数列的前n项和写出总数，根据所给的m个珠子排成的图形，写出方程组，解方程组即可．

解答：解：由题意知当用珠子排成正三角形数组时，当边上只有一个珠子时，共有一个珠子，
当边上有两个珠子时，共有3个珠子，
当边上有三个珠子时，有6个珠子，
以此类推当边上有n个珠子时，共有1+2+3+4+…+n=

n(n+1)

2

，
用珠子排成正四边形的数组时，
当边上有1个珠子，共有一个，
…
当一边上有n个珠子时，共有1+3+5+7+…+2n-1=n²，
当用珠子排成正五边形时，当一条边上有n个珠子时，共有

n(3n-1)

2

，
∵m个钢珠恰好可以排成每边n个钢珠的正三角形数组与正方形数组各一个；
且知若用这m个钢珠去排成每边n个钢珠的正五边形数组时，就会多出9个钢珠，
∴

n(n+1)

2

+n2= m，①
 

n(3n-1)

2

+9=m    ②
把②代入①得到n=9，
代入①得到m=126，
故答案为：126

点评：考查等差数列的前n项和，考查观察图形，考查方程思想的应用，是一个综合题目，这种题目具有创新性，是一个好题又是一个易错题．