网址:http://m.1010jiajiao.com/timu_id_160059[举报]
一、BDCBA,BDCDC,BB
二、13. 14.8; 15.; 16. ③④
三、17、
解:(Ⅰ)
……………2分
由题意知对任意实数x恒成立,
得,
………………………………………………………6分
(Ⅱ)由(Ⅰ)知
由,解得
所以,的单调增区间为……………………12分
18、
解:(Ⅰ)证明取SC的中点R,连QR, DR.。
由题意知:PD∥BC且PD=BC;
QR∥BC且QP=BC,
QR∥PD且QR=PD。
PQ∥PR,又PQ面SCD,PQ∥面SCD. …………6分
(Ⅱ)法一:
…………12分
(Ⅱ)法二:以P为坐标原点,PA为x轴,PB为y轴,PS为z轴建立空间直角坐标系,则S(),B(),C(),Q(),
面PBC的法向量为(),设为面PQC的法向量,
由
COS
…………12分
19、解
设A,B两点的坐标为()、()则
(Ⅰ)经过A、B两点的直线方程为
由得:
令得:
从而
(否则,有一个为零向量)
代入(1)得
始终经过这个定点 …………………(6分)
(Ⅱ)设AB中点的坐标为(),则
又
即
AB的中点到直线的距离d为:
因为d的最小值为 ……………(12分)
20、解:(Ⅰ)密码中不同数字的个数为2的事件为密码中只有两个数字,注意到密码的第1,2列分别总是1,2,即只能取表格第1,2列中的数字作为密码.
…………………………………………………………………4分
(Ⅱ)由题意可知,ξ的取值为2,3,4三种情形.
若ξ= 3,注意表格的第一排总含有数字1,第二排总含有数字2则密码中只可能取数字1,2,3或1,2,4.
若
(或用求得). ………………………………………………8分
的分布列为:
ξ
2
3
4
p
……………………………………………12分
21、
(Ⅰ)
时,,即
当时,
即
在上是减函数的充要条件为 ………(4分)
(Ⅱ)由(Ⅰ)知,当时为减函数,的最大值为;
当时,
当时,当时
即在上是增函数,在上是减函数,时取最大值,最大值为
即 ………………(9分)
(Ⅲ)在(Ⅰ)中取,即
由(Ⅰ)知在上是减函数
,即
,解得:或
故所求不等式的解集为[ ……………(13分)
22、
解::⑴
,
,即为的表达式。 (6分)
⑵,,又()
要使成立,只要,即,
即为所求。
⑶
故有
(13分)
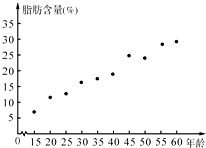 在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据,并制作成如图所示的人体脂肪含量与年龄关系的散点图.根据该图,下列结论中正确的是( )
在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据,并制作成如图所示的人体脂肪含量与年龄关系的散点图.根据该图,下列结论中正确的是( )| A、人体脂肪含量与年龄正相关,且脂肪含量的中位数等于20% | B、人体脂肪含量与年龄正相关,且脂肪含量的中位数小于20% | C、人体脂肪含量与年龄负相关,且脂肪含量的中位数等于20% | D、人体脂肪含量与年龄负相关,且脂肪含量的中位数小于20% |
在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据,并制作成如图所示的人体脂肪含量与年龄关系的散点图.根据该图,下列结论中正确的是( )
| A.人体脂肪含量与年龄正相关,且脂肪含量的中位数等于20% |
| B.人体脂肪含量与年龄正相关,且脂肪含量的中位数小于20% |
| C.人体脂肪含量与年龄负相关,且脂肪含量的中位数等于20% |
| D.人体脂肪含量与年龄负相关,且脂肪含量的中位数小于20% |
| A.人体脂肪含量与年龄正相关,且脂肪含量的中位数等于20% |
| B.人体脂肪含量与年龄正相关,且脂肪含量的中位数小于20% |
| C.人体脂肪含量与年龄负相关,且脂肪含量的中位数等于20% |
| D.人体脂肪含量与年龄负相关,且脂肪含量的中位数小于20% |
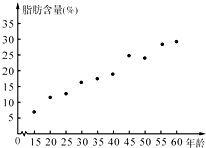
(08年安庆一中三模理) 在一次对人体脂肪含量和年龄关系的研究中,研究人员获得了一组样本数据:
人体的脂肪含量百分比和年龄
年龄 | 23 | 27 | 39 | 41 | 45 | 49 | 50 | 53 | 56 | 58 | 60 |
脂肪 | 9.5 | 17.8 | 21.2 | 25.9 | 27.5 | 26.3 | 28.2 | 29.6 | 31.4 | 33.5 | 35.2 |
通过计算得到回归方程为![]() ,利用这个方程,我们得到年龄37岁时体内脂肪含量为20.90%,那么数据20.90%的意义是:
,利用这个方程,我们得到年龄37岁时体内脂肪含量为20.90%,那么数据20.90%的意义是:
A 某人年龄37岁,他体内脂肪含量为20.90%;
B 某人年龄37岁,他体内脂肪含量为20.90%的概率最大;
C 某人年龄37岁,他体内脂肪含量的期望值为20.90%;
D 20.90%是对年龄为37岁的人群中的大部分人的体内脂肪含量所作出的估计;
查看习题详情和答案>>