摘要:化简得(当时也满足).
网址:http://m.1010jiajiao.com/timu_id_159997[举报]
请先阅读:
设可导函数 f(x) 满足f(-x)=-f(x)(x∈R).
在等式f(-x)=-f(x) 的两边对x求导,
得(f(-x))′=(-f(x))′,
由求导法则,得f′(-x)•(-1)=-f′(x),
化简得等式f′(-x)=f′(x).
(Ⅰ)利用上述想法(或其他方法),结合等式(1+x)n=
+
x+
x2+…+
xn(x∈R,整数n≥2),证明:n[(1+x)n-1-1]=2
x+3
x2+4
x3+…+n
xn-1;
(Ⅱ)当整数n≥3时,求
-2
+3
-…+(-1)n-1n
的值;
(Ⅲ)当整数n≥3时,证明:2
-3•2
+4•3
+…+(-1)n-2n(n-1)
=0.
查看习题详情和答案>>
设可导函数 f(x) 满足f(-x)=-f(x)(x∈R).
在等式f(-x)=-f(x) 的两边对x求导,
得(f(-x))′=(-f(x))′,
由求导法则,得f′(-x)•(-1)=-f′(x),
化简得等式f′(-x)=f′(x).
(Ⅰ)利用上述想法(或其他方法),结合等式(1+x)n=
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | 2 n |
| C | 3 n |
| C | 4 n |
| C | n n |
(Ⅱ)当整数n≥3时,求
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
(Ⅲ)当整数n≥3时,证明:2
| C | 2 n |
| C | 3 n |
| C | 4 n |
| C | n n |
请先阅读:
设可导函数 f(x) 满足f(-x)=-f(x)(x∈R).
在等式f(-x)=-f(x) 的两边对x求导,
得(f(-x))′=(-f(x))′,
由求导法则,得f′(-x)•(-1)=-f′(x),
化简得等式f′(-x)=f′(x).
(Ⅰ)利用上述想法(或其他方法),结合等式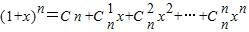 (x∈R,整数n≥2),证明:
(x∈R,整数n≥2),证明: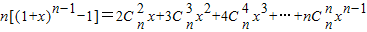 ;
;
(Ⅱ)当整数n≥3时,求 的值;
的值;
(Ⅲ)当整数n≥3时,证明: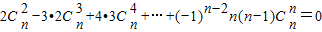 .
.
查看习题详情和答案>>
设可导函数 f(x) 满足f(-x)=-f(x)(x∈R).
在等式f(-x)=-f(x) 的两边对x求导,
得(f(-x))′=(-f(x))′,
由求导法则,得f′(-x)•(-1)=-f′(x),
化简得等式f′(-x)=f′(x).
(Ⅰ)利用上述想法(或其他方法),结合等式
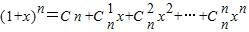 (x∈R,整数n≥2),证明:
(x∈R,整数n≥2),证明: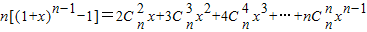 ;
;(Ⅱ)当整数n≥3时,求
 的值;
的值;(Ⅲ)当整数n≥3时,证明:
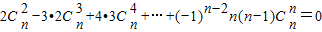 .
.查看习题详情和答案>>
请先阅读:
设可导函数 f(x) 满足f(-x)=-f(x)(x∈R).
在等式f(-x)=-f(x) 的两边对x求导,
得(f(-x))′=(-f(x))′,
由求导法则,得f′(-x)•(-1)=-f′(x),
化简得等式f′(-x)=f′(x).
(Ⅰ)利用上述想法(或其他方法),结合等式(1+x)n=
+
x+
x2+…+
xn(x∈R,整数n≥2),证明:n[(1+x)n-1-1]=2
x+3
x2+4
x3+…+n
xn-1;
(Ⅱ)当整数n≥3时,求
-2
+3
-…+(-1)n-1n
的值;
(Ⅲ)当整数n≥3时,证明:2
-3•2
+4•3
+…+(-1)n-2n(n-1)
=0.
查看习题详情和答案>>
设可导函数 f(x) 满足f(-x)=-f(x)(x∈R).
在等式f(-x)=-f(x) 的两边对x求导,
得(f(-x))′=(-f(x))′,
由求导法则,得f′(-x)•(-1)=-f′(x),
化简得等式f′(-x)=f′(x).
(Ⅰ)利用上述想法(或其他方法),结合等式(1+x)n=
| C | 0n |
| C | 1n |
| C | 2n |
| C | nn |
| C | 2n |
| C | 3n |
| C | 4n |
| C | nn |
(Ⅱ)当整数n≥3时,求
| C | 1n |
| C | 2n |
| C | 3n |
| C | nn |
(Ⅲ)当整数n≥3时,证明:2
| C | 2n |
| C | 3n |
| C | 4n |
| C | nn |
 上动点
上动点 到定点
到定点 与定直线
与定直线 的距离之比为常数
的距离之比为常数 .
. 引曲线C的弦AB恰好被点
引曲线C的弦AB恰好被点 平分,求弦AB所在的直线方程;
平分,求弦AB所在的直线方程; 为圆心作圆
为圆心作圆 ,设圆
,设圆 与点
与点 ,求
,求 的最小值,并求此时圆
的最小值,并求此时圆 作直线
作直线 的垂线,垂足为D.
的垂线,垂足为D. 代入坐标得到
代入坐标得到 ;,化简得
;,化简得
 ,, 不妨设
,, 不妨设 .
. .
.
 ,则
,则 ,
, ,故当
,故当 时,
时, 取得最小值为
取得最小值为 .
. ,故
,故 ,又点
,又点 在圆
在圆 上,代入圆的方程得到
上,代入圆的方程得到 .
. 