摘要：∴f(n)=3?()n-1.由公比不为1的等比数列的前n项和公式,得
网址：http://m.1010jiajiao.com/timu_id_15784[举报]
设f（x）是定义在实数R上的函数，g（x）是定义在正整数N*上的函数，同时满足下列条件：
（1）任意x，y∈R，有f（x+y）=f（x）f（y），当x＜0时，f（x）＞1且f(-1)=
；
（2）g（1）=f（0），g（2）=f（-2）；
（3）f[g(n+2)]=
，n∈N*
试求：
（1）证明：任意x，y∈R，x≠y，都有
＜0；
（2）是否存在正整数n，使得g（n）是25的倍数，若存在，求出所有自然数n；若不存在说明理由．（阶乘定义：n!=1×2×3×…×n）
查看习题详情和答案>>
（1）任意x，y∈R，有f（x+y）=f（x）f（y），当x＜0时，f（x）＞1且f(-1)=
| 5 |
（2）g（1）=f（0），g（2）=f（-2）；
（3）f[g(n+2)]=
| f[(n+3)g(n+1)] |
| f[(n+2)g(n)] |
试求：
（1）证明：任意x，y∈R，x≠y，都有
| f(x)-f(y) |
| x-y |
（2）是否存在正整数n，使得g（n）是25的倍数，若存在，求出所有自然数n；若不存在说明理由．（阶乘定义：n!=1×2×3×…×n）
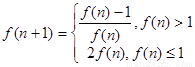，若对任意的
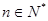，总有f(n+3)=f(n)成立，则a在
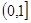内的可能值有（ ）个。
(
+3),Tn=
+
+
+…+
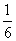,求证:
≤Tn≤
(n∈N*).